题目内容
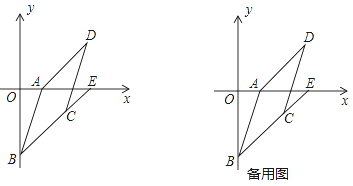
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)连结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标.
【答案】
(1)
解:∵抛物线y=ax2+bx﹣5与y轴交于点C,
∴C(0,﹣5),
∴OC=5.
∵OC=5OB,
∴OB=1,
又点B在x轴的负半轴上,
∴B(﹣1,0).
∵抛物线经过点A(4,﹣5)和点B(﹣1,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴这条抛物线的表达式为y=x2﹣4x﹣5.

(2)
解:由y=x2﹣4x﹣5,得顶点D的坐标为(2,﹣9).
连接AC,
∵点A的坐标是(4,﹣5),点C的坐标是(0,﹣5),
又S△ABC= ![]() ×4×5=10,S△ACD=
×4×5=10,S△ACD= ![]() ×4×4=8,
×4×4=8,
∴S四边形ABCD=S△ABC+S△ACD=18.
(3)
解:过点C作CH⊥AB,垂足为点H.
∵S△ABC= ![]() ×AB×CH=10,AB=5
×AB×CH=10,AB=5 ![]() ,
,
∴CH=2 ![]() ,
,
在RT△BCH中,∠BHC=90°,BC= ![]() ,BH=
,BH= ![]() =3
=3 ![]() ,
,
∴tan∠CBH= ![]() =
= ![]() .
.
∵在RT△BOE中,∠BOE=90°,tan∠BEO= ![]() ,
,
∵∠BEO=∠ABC,
∴ ![]() ,得EO=
,得EO= ![]() ,
,
∴点E的坐标为(0, ![]() )
)
【解析】(1)先得出C点坐标,再由OC=5BO,得出B点坐标,将A、B两点坐标代入解析式求出a,b;(2)分别算出△ABC和△ACD的面积,相加即得四边形ABCD的面积;(3)由∠BEO=∠ABC可知,tan∠BEO=tan∠ABC,过C作AB边上的高CH,利用等面积法求出CH,从而算出tan∠ABC,而BO是已知的,从而利用tan∠BEO=tan∠ABC可求出EO长度,也就求出了E点坐标.
【考点精析】本题主要考查了二次函数的概念和二次函数的图象的相关知识点,需要掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案