Question

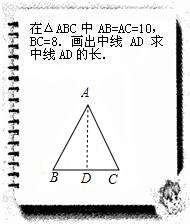文文和彬彬在完成作业，“如图在△ABC中，AB=AC=10，BC=8．画出中线AD并求中线AD的长．”时她们对各自所作的中线AD描述如图：
文文：“过点A作BC的垂线AD，垂足为D，AD就是△ABC的中线”；
彬彬：“作△ABC的角平分线AD，AD就是△ABC的中线”．那么：
（1）上述作法你认为是两位同学的作法谁的较好？
（2）请你根据中线作法帮她求出AD的长？

Answer 1

分析：两人的作法都正确，因为等腰三角形中三线合一的定理，中线和垂线及角平分线是一条直线．
根据勾股定理可求出AD的长．

解答：解：（1）文文的作法较好（或彬彬的较好）
根据三线合一的定理．

（2）在△ABC中，AB=AC，AD⊥BC，
∴AD是△ABC的中线，
BD=CD=

1

2

BC=

1

2

×8=4．
在Rt△ABD中，AB=10，BD=4，AD²+BD²=AB²，
∴AD=

AB2-BD2

=

102-42

=2

21

．

点评：本题主要考查了三线合一的定理．