��Ŀ����
����Ŀ��̩����Ϊ��һ��������̬���������Խֵ������̻����裬Ϊ���������ס���������ľ����֪������ľ�ĵ���Ϊ![]() Ԫ��������ľ�ĵ���Ϊ
Ԫ��������ľ�ĵ���Ϊ![]() Ԫ.
Ԫ.
(1)��![]() �ֵ�����ס���������ľ������
�ֵ�����ס���������ľ������![]() Ԫ�����У�������ľ�Ǽ�����ľ��һ���
Ԫ�����У�������ľ�Ǽ�����ľ��һ���![]() �ã�������ýֵ�����ļס���������ľ�����ٿã�
�ã�������ýֵ�����ļס���������ľ�����ٿã�
(2)������ϱ�����������ľ�ijɻ���Ϊ![]() ��������ľ�ijɻ���Ϊ
��������ľ�ijɻ���Ϊ![]() .��
.��![]() �ֵ�����ס���������ľ��
�ֵ�����ס���������ľ��![]() �ã�Ϊ��ʹ������ľ���ܳɻ��ʲ�����
�ã�Ϊ��ʹ������ľ���ܳɻ��ʲ�����![]() ���������ľ�������ٿã�
���������ľ�������ٿã�
���𰸡���1��������ľ��![]() �ã�������ľ
�ã�������ľ![]() �ã���2��������ľ�����
�ã���2��������ľ�����![]() .
.
��������
��1���������ľx�ã�������y�ã��ؼ�������ס���������ľ������34000Ԫ�����У�������ľ�Ǽ�����ľ��һ���120�ã����ݵ�����ϵ�г����̲����
��2����������繺��a�ã����������繺��500-a���ã���������ɵò��ȹ�ϵ����������ijɻ���+��������ijɻ�����92%��500����ɵô𰸣�
��1���������ľ��![]() �ã�������ľ��
�ã�������ľ��![]() �ã��������⣬��
�ã��������⣬��
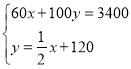
��ã�![]()
�𣺼�����ľ��![]() �ã�������ľ
�ã�������ľ![]() ��.
��.
��2����������繺��a�ã����������繺��800-a���ã�������ã�
90%a+95%��500-a����92%��500��
��ã�a��300��
��a������
��a=300��
�𣺼������������300�ã�