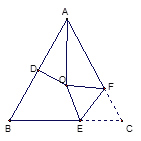
题目内容
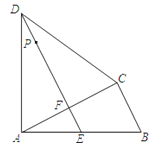
【题目】已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.
(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE=![]() AD,EF=2
AD,EF=2![]() , 求线段CG的长.
, 求线段CG的长.
【答案】证明:(1)如图1,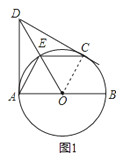
连接OC,
∵DA、DC分别是⊙O的切线,点A、C是切点,OA、OC是半径,
∴OA⊥DA,OC⊥DC,
∴∠DAO=∠DCO=90°,
在Rt△ODA和Rt△ODC中,![]() ,
,
∴Rt△ODA≌Rt△ODC,
∴∠EOA=∠EOC,
∴AE=CE;
(2)证明:如图2,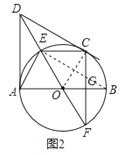
连接OC,BE,由(1)证得∠AOE=∠COE,
又∵∠B=![]() ∠AOE,∠F=
∠AOE,∠F=![]() ∠COE,
∠COE,
∴∠B=∠F,
∵OB=OE,
∴∠B=∠OEB,
∴∠F=∠OEG,
∵∠EGC是△EGF的外角,
∴∠EGC=∠F+∠GEF=2∠F,
即∠EGC=2∠F;
(3)解:∵EF是⊙O的直径,
∴∠ECF=90°
∵EF=2![]() ,
,
∴OA=OE=![]() EF=
EF=![]() ,
,
∵DE=![]() AD,设DE=m,
AD,设DE=m,
∴AD=2m,
在Rt△DAO中,OA2+DA2=OD2 ,
∴![]() ,
,
解得m1=0(舍去),m2=![]() ,
,
∴DA=![]()
![]() ,DO=
,DO=![]()
![]() ,
,
∴在Rt△ADO中,tan∠DOA=![]() =
=![]() ,cos∠DOA=
,cos∠DOA=![]() =
=![]() ,
,
∵∠EOA=2∠B,∠EGC=2∠F,
∴∠EGC=∠EOA,
∴tan∠EGC=![]() ,
,
如图3,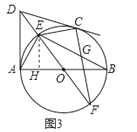
过点E作EH⊥AB于点H,
在Rt△EOH中OH=OEcos∠EOH=![]() X
X![]() =
=![]()
![]() ,
,
∴EH=![]()
![]() AH=AO﹣OH=
AH=AO﹣OH=![]() -
-![]()
![]() =
=![]()
![]() ,
,
在Rt△EHA中,EA2=AH2+EH2 ,
∴EA=2,
∵AE=CE,
∴EC=2,
在Rt△ECG中,tan∠EGC=![]() =
=![]() =
=![]() ,
,
∴GC=![]() .
.
【解析】(1)连接OC,根据切线的性质得到OA⊥DA,OC⊥DC,由垂直的定义得到∠DAO=∠DCO=90°,推出Rt△ODA≌Rt△ODC,根据全等三角形的性质得到∠EOA=∠EOC,由等腰三角形的判定得到结论;
(2)连接OC,BE,由(1)证得∠AOE=∠COE,根据圆周角定理得到∠B=![]() ∠AOE,∠F=
∠AOE,∠F=![]() ∠COE,得到∠B=∠F,根据等腰三角形的性质得到∠B=∠OEB,于是得到∠F=∠OEG,根据三角形的外角的性质即可得到结论;
∠COE,得到∠B=∠F,根据等腰三角形的性质得到∠B=∠OEB,于是得到∠F=∠OEG,根据三角形的外角的性质即可得到结论;
(3)由圆周角定理得到∠ECF=90°求得OA=OE=![]() EF=
EF=![]() , 设DE=m,AD=2m,根据勾股定理列方程得到m1=0(舍去),m2=
, 设DE=m,AD=2m,根据勾股定理列方程得到m1=0(舍去),m2=![]() , 于是得到DA=DA=
, 于是得到DA=DA=![]()
![]() , DO=
, DO=![]()
![]() , 在Rt△ADO中,tan∠DOA=
, 在Rt△ADO中,tan∠DOA=![]() =
=![]() , cos∠DOA=
, cos∠DOA=![]() =
=![]() , 得到tan∠EGC=
, 得到tan∠EGC=![]() , 过点E作EH⊥AB于点H,在Rt△EOH中OH=OEcos∠EOH=
, 过点E作EH⊥AB于点H,在Rt△EOH中OH=OEcos∠EOH=![]() X
X![]() =
=![]()
![]() , 于是得到EH=
, 于是得到EH=![]()
![]() AH=AO﹣OH=
AH=AO﹣OH=![]() -
-![]()
![]() =
=![]()
![]() , 根据勾股定理求得EC=2,根据三角函数的定义即可得到结论.
, 根据勾股定理求得EC=2,根据三角函数的定义即可得到结论.