题目内容
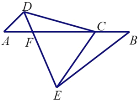
【题目】如图，C是AB上一点，点D、E分别位于AB的异侧，AD∥BE，且AD=BC，AC=BE．
（1）求证：CD=CE；
（2）当
时，求BF的长；
（3）若∠A=α，∠ACD=25°，且△CDE的外心在该三角形的外部，请直接写出α的取值范围．
【答案】（1）见解析；（2）
；（3）
【解析】
（1）根据全等三角形的判定，证明
，即可得到结论；
（2）由（1）的结论，结合三角形的外角性质，得到
，然后得到
，即可得到答案；
（3）根据题意，先用
表示出∠DCE，然后判断△DCE为钝角三角形，结合等腰三角形和钝角三角形的性质，即可求出的取值范围.
解：（1）∵
，
∴
，
又∵
，
，
∴，
∴
；
（2）由（1）知
，
，
∴
，
∴
，
∴，
∴
；
（3）∵
，
，
∴
，
∵
的外心在该三角形的外部，
∴为钝角三角形，
由（2）知为等腰三角形，
∴
为钝角，
∴
，
∴．
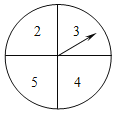
【题目】如图所示，有一个可以自由转动的转盘，其盘面分为4等份，在每一等份分别标有对应的数字2，3，4，5．小明打算自由转动转盘10次，现已经转动了8次，每一次停止后，小明将指针所指数字记录如下：
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
（1）求前8次的指针所指数字的平均数．
（2）小明继续自由转动转盘2次，判断是否可能发生“这10次的指针所指数字的平均数不小于3.3，且不大于3.5”的结果？若有可能，计算发生此结果的概率，并写出计算过程；若不可能，说明理由．（指针指向盘面等分线时为无效转次．）
【题目】受地震的影响，某超市鸡蛋供应紧张，需每天从外地调运鸡蛋1200斤．超市决定从甲、乙两大型养殖场调运鸡蛋，已知甲养殖场每天最多可调出800斤，乙养殖场每天最多可调出900斤，从两养殖场调运鸡蛋到超市的路程和运费如表：
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元，则从甲、乙两养殖场各调运了多少斤鸡蛋？
(2)设从甲养殖场调运鸡蛋x斤，总运费为W元，试写出W与x的函数关系式，怎样安排调运方案才能使每天的总运费最省？
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛，试卷题目共10题，每题10分．现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100．
整理数据：
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据：
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题：
（1）请直接写出表格中
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；
（3）为了让学生重视安全知识的学习，学校将给竞赛成绩满分的同学颁发奖状，该校七年级新生共570人，试估计需要准备多少张奖状？