题目内容
 如图所示,正比例函数y=x与反比例函数y=
如图所示,正比例函数y=x与反比例函数y=| k |
| x |
分析:首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|,得出S△AOB=S△ODC=
,再根据反比例函数的对称性可知:OB=OD,得出S△ADB+S△BDC得出结果.
| 1 |
| 2 |
| |k| |
| 2 |
解答:解:根据反比例函数的对称性可知:OB=OD,AB=CD,
∵四边形ABCD的面积等于S△ADB+S△BDC,
∵A(x,
),B(x,0),C(-x,-
),D(-x,0)
∴S△ADB=
(DO+OB)×AB=
×2x×
=k,
S△BDC=
(DO+OB)×DC=
×2x×
=k,
∴四边形ABCD的面积=2k.
故选B.
∵四边形ABCD的面积等于S△ADB+S△BDC,
∵A(x,
| k |
| x |
| k |
| x |
∴S△ADB=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
∴四边形ABCD的面积=2k.
故选B.
点评:主要考查了反比例函数y=kx中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|.
| 1 |
| 2 |

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
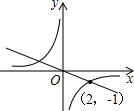 如图所示,正比例函数y=k1x与反比例函数y=
如图所示,正比例函数y=k1x与反比例函数y= 13、如图所示,正比例函数y1=kx与一次函数y2=-x+a的图象交于点A,根据图上给出的条件,回答下列问题:
13、如图所示,正比例函数y1=kx与一次函数y2=-x+a的图象交于点A,根据图上给出的条件,回答下列问题: 已知:如图所示,正比例函数y=ax的图象与反比例函数y=
已知:如图所示,正比例函数y=ax的图象与反比例函数y= 如图所示,正比例函数y=kx(k>0)与反比例函数y=
如图所示,正比例函数y=kx(k>0)与反比例函数y=