题目内容
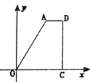
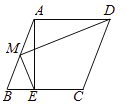
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上两动点,且
上两动点,且![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
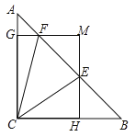
(1)求证:![]() ;
;
(2)试探究![]() 、
、![]() 、
、![]() 之间有何数量关系?说明理由.
之间有何数量关系?说明理由.
【答案】(1)见解析;(2)![]() ,理由见解析
,理由见解析
【解析】
(1)由已知得出∠A=∠5=45°,再证得∠7=∠ACE,即可得出△ACE∽△BFC;
(2)将△ACF顺时针旋转90°至△BCD,由旋转的性质得出CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF,证得∠DCE=∠2,由SAS可证△ECF≌△ECD,得出EF=DE,证得∠EBD=90°,由勾股定理即可得出结论.
解:(1)证明:∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵![]() ,
,![]() ,
,
∴![]() ,
,
将![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,如图所示:
,如图所示:

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目