题目内容
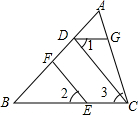如图，已知在△ABC中，EF平行于CD，G在AC边上，∠1=∠2，求证：∠AGD=∠ACB．
证明：∵EF∥CD，
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴DG∥BC，
∴∠AGD=∠ACB．
分析：由EF与CD平行，利用两直线平行同位角相等得到一对角相等，由已知角相等等量代换得到一对内错角相等，利用内错角相等两直线平行，利用两直线平行同位角相等即可得证．
点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴DG∥BC，
∴∠AGD=∠ACB．
分析：由EF与CD平行，利用两直线平行同位角相等得到一对角相等，由已知角相等等量代换得到一对内错角相等，利用内错角相等两直线平行，利用两直线平行同位角相等即可得证．
点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知在△ABC中，BD为∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD于M，PN⊥CD于N，求证：PM=PN．
如图，已知在△ABC中，AB=AC，∠A=100°，CD是∠ACB的平分线．
如图，已知在△ABC中，∠B与∠C的平分线交于点P．当∠A=70°时，则∠BPC的度数为
如图，已知在△ABC中，CD=CE，∠A=∠ECB，试说明CD2=AD•BE．