Question

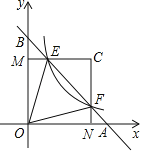
【题目】如图，已知在矩形中，，，，分别是四个内角的平分线，，相交于点，，相交于点求证：四边形是正方形．

Answer 1

【答案】见解析．

【解析】

根据矩形的性质和角平分线定义易得△FDC、△MDA、△EAB、△NBC都是等腰直角三角形，则∠E＝∠F＝∠EMF＝∠ENF＝90°，可得四边形EMFN是矩形，然后证明△FDC≌△EAB，求出ME＝MF即可证得结论．

证明：∵在矩形ABCD中，，，，分别是四个内角的平分线，

∴∠FDC＝∠FCD＝45°，

∴△FDC是等腰直角三角形，

同理可得：△MDA、△EAB、△NBC都是等腰直角三角形，

∴∠E＝∠F＝∠EMF＝∠ENF＝90°，

∴四边形EMFN是矩形，

在△FDC和△EAB中，，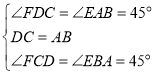

∴△FDC≌△EAB（ASA），

∴FD＝EA，

又∵MD＝MA，

∴ME＝MF，

∴矩形EMFN是正方形．