Question

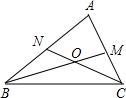如图，△ABC的角平分线BM，CN相交于O．
求证：点O到三边AB、BC、CA的距离相等．

Answer 1

证明：作OD、OE、OF分别垂直于三边AB、BC、CA，
D、E、F为垂足，
∵BM为△ABC的角平分线，
OD⊥AB，OE⊥BC，
∴OD=OE（角平分线上的点到这个角两边的距离相等）．
同理可证：OF=OE．
∴OD=OE=OF．
即点O到三边AB、BC、CA的距离相等．
分析：作OD、OE、OF分别垂直于三边AB、BC、CA，D、E、F为垂足，根据角平分线性质可得OD=OE，OF=OE，∴OD=OE=OF．
点评：此题主要考查角平分线的性质：角平分线上的点到这个角两边的距离相等．正确作出辅助线是解答本题的关键．