题目内容
PA、PB是⊙O的两条切线,⊙O的半径是5,OP=10,那么∠APB等于
- A.120°
- B.90°
- C.60°
- D.30°
C
分析:设点A、B为切点,连OA,OB,根据切线的性质和切线长定理得到OA⊥PA,OB⊥PB,∠1=∠2,在Rt△APO中,OA=5,OP=10,根据三角函数得到sin∠1= =
= ,
,
则∠1=30°,即可得到∠APB的度数.
解答: 解:设点A、B为切点,连OA,OB,如图,
解:设点A、B为切点,连OA,OB,如图,
∴OA⊥PA,OB⊥PB,∠1=∠2,
在Rt△APO中,
∵OA=5,OP=10,
∴sin∠1= =
= ,
,
∴∠1=30°,
∴∠2=30°,
∴∠APB=60°.
故选C.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了切线长定理以及三角函数的定义和特殊角的三角函数值.
分析:设点A、B为切点,连OA,OB,根据切线的性质和切线长定理得到OA⊥PA,OB⊥PB,∠1=∠2,在Rt△APO中,OA=5,OP=10,根据三角函数得到sin∠1=
 =
= ,
,则∠1=30°,即可得到∠APB的度数.
解答:
 解:设点A、B为切点,连OA,OB,如图,
解:设点A、B为切点,连OA,OB,如图,∴OA⊥PA,OB⊥PB,∠1=∠2,
在Rt△APO中,
∵OA=5,OP=10,
∴sin∠1=
 =
= ,
,∴∠1=30°,
∴∠2=30°,
∴∠APB=60°.
故选C.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了切线长定理以及三角函数的定义和特殊角的三角函数值.

练习册系列答案
相关题目
 如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为( )
如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为( )A、
| ||
B、
| ||
C、
| ||
D、
|
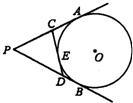 7、如图,PA、PB是⊙O的两条切线,A、B是切点,CD切劣弧AB于点E,已知切线PA的长为6cm,则△PCD的周长为
7、如图,PA、PB是⊙O的两条切线,A、B是切点,CD切劣弧AB于点E,已知切线PA的长为6cm,则△PCD的周长为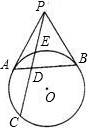 如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE=2,CD=1,求DE的长.
如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE=2,CD=1,求DE的长.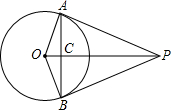 如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=
如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=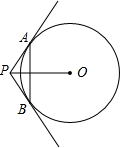 如图,直线PA,PB是⊙O的两条切线,A,B分别为切点,∠APB=120°,OP=10厘米,则弦AB的长为
如图,直线PA,PB是⊙O的两条切线,A,B分别为切点,∠APB=120°,OP=10厘米,则弦AB的长为