题目内容
如图,已知△ABC中,∠B=90 º,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间(只要直接写出答案).
(1) cm (2)
cm (2) =
= (3)
(3) =5.5或6或6.6 .
=5.5或6或6.6 .
【解析】
试题分析:(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)设出发 秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=
秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ= ,BP=
,BP= ,列式求得
,列式求得 即可;
即可;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:①当CQ=BQ时(图1),则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得 ;
;
②当CQ=BC时(如图2),则BC+CQ=12,易求得 ;
;
③当BC=BQ时(如图3),过B点作BE⊥AC于点E,则求出BE,CE,即可得出 .
.
试题解析:(1)BQ=2×2=4cm,BP=AB﹣AP=8﹣2×1=6cm,∵∠B=90°,
PQ= ;
;
(2)BQ= ,BP=
,BP= ,
, ,解得:
,解得: ;
;
(3)①当CQ=BQ时(图1),则∠C=∠CBQ,∵∠ABC=90°,∴∠CBQ+∠ABQ=90°,∠A+∠C=90°,∴∠A=∠ABQ,∴BQ=AQ,∴CQ=AQ=5,∴BC+CQ=11,∴ =11÷2=5.5秒.
=11÷2=5.5秒.

②当CQ=BC时(如图2),则BC+CQ=12,∴ =12÷2=6秒.
=12÷2=6秒.

③当BC=BQ时(如图3),过B点作BE⊥AC于点E,则BE= ,所以CE=
,所以CE= ,故CQ=2CE=7.2,所以BC+CQ=13.2,∴
,故CQ=2CE=7.2,所以BC+CQ=13.2,∴ =13.2÷2=6.6秒.
=13.2÷2=6.6秒.
由上可知,当 为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.

考点:1.勾股定理;2.等腰三角形的判定与性质;3.动点型.

 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.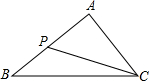 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )