题目内容
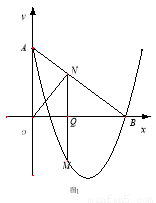
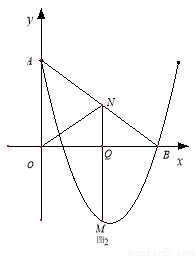
如图1,在平面直角坐标系中,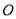 为坐标原点.直线
为坐标原点.直线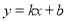 与抛物线
与抛物线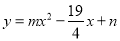 同时经过
同时经过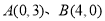 .
.

(1)求 的值.
的值.
(2)点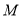 是二次函数图象上一点,(点
是二次函数图象上一点,(点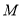 在
在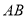 下方),过
下方),过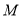 作
作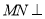
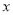 轴,与
轴,与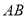 交于点
交于点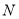 ,与
,与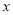 轴交于点
轴交于点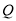 .求
.求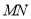 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点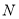 ,使
,使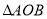 和
和 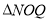 相似?若存在,求出
相似?若存在,求出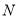 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
(1)m=1,n=3;(2)4;(3)N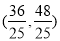 或N
或N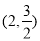 .
.
【解析】
试题分析:(1)应用待定系数法求抛物线的解析式中的m和n的值;
(2)求出一次函数解析式,联系点的坐标的几何意义表示线段MN的长,根据所列关系式求最大值;
(3)分两种情况讨论,当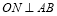 时,得到
时,得到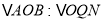 ,计算OQ和NQ的值,得点N的坐标;当N为AB中点时,得到
,计算OQ和NQ的值,得点N的坐标;当N为AB中点时,得到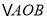 ∽
∽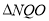 ,进而得到点N的坐标.
,进而得到点N的坐标.
试题解析:【解析】
(1)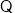 抛物线
抛物线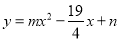 经过两点
经过两点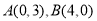 ,
,
∴ ,解得:
,解得: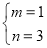 ,
,
所以m的值为1,n的值为3,此时二次函数的表达式为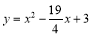 .
.
(2)把点A(0,3),点B(4,0)代入y=kx+b,得:
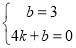 ,解得:
,解得: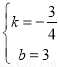 ,
,
∴经过A、B两点的一次函数的解析式为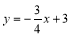 .
.
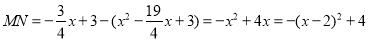 ,
,
∵0≤x≤4,∴ 当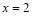 时,
时,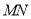 取得最大值为4.
取得最大值为4.
(3)存在.
①当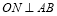 时,(如图1)
时,(如图1)
可证: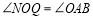 ,
,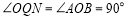 ,
,
∴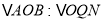 ,
,
∴ 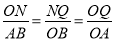 ,
,
∵OA=3,OB=4,
∴AB=5,
∵ON·AB=OA·OB,
∴ON=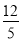 ,
,
∴NQ=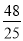 ,OQ=
,OQ=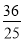 ,
,
∴N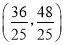 ;
;
②当N为AB中点时,(如图2)
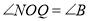 ,
,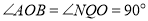
∴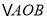 ∽
∽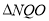 ,此时
,此时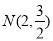 .
.
∴满足条件的N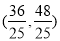 或N
或N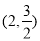 .
.
考点:1、待定系数法求解析式;2、图形与坐标;3、相似三角形的判定和性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的一元二次方程的是
的一元二次方程的是  B.
B.
 D.
D. 
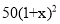 =182 B.50+50(1+x)+
=182 B.50+50(1+x)+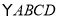 中,
中,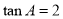 ,
,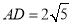 ,
, ,
, 是
是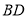 中点,
中点,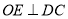 于
于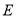 .
.
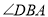 的度数.
的度数.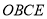 的面积.
的面积.  .
.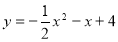 ,
, 取何值时,
取何值时, 随
随 轴上方?
轴上方? 、
、 、
、 、
、 、
、 中分式的个数有( ).
中分式的个数有( ).