题目内容
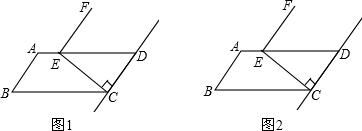
在□ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90°得到线段EF(如图(1))。
(1)在图(1)中画图探究:
①当P1为射线CD上任意一点(P不与C点重合)时,连接EP1,将线段EP,绕点E逆时针旋转90°得到线段EC1,判断直线FG1与直线CD的位置关系并加以证明;
②当P2为线段DC的延长线上任意一点时,连接EP2,将线段EP2绕点E逆时针旋转90°得到线段EG2,判断直线G1G2与直线CD的位置关系, 画出图形并直接写出你的结论;
(2)若AD=6,tanB=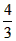 ,AE=1,在①的条件下,设CP1=x,
,AE=1,在①的条件下,设CP1=x,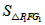 =y,求y与x之间的函数关系式,并写出自变量x的取值范围。
=y,求y与x之间的函数关系式,并写出自变量x的取值范围。
(1)在图(1)中画图探究:
①当P1为射线CD上任意一点(P不与C点重合)时,连接EP1,将线段EP,绕点E逆时针旋转90°得到线段EC1,判断直线FG1与直线CD的位置关系并加以证明;
②当P2为线段DC的延长线上任意一点时,连接EP2,将线段EP2绕点E逆时针旋转90°得到线段EG2,判断直线G1G2与直线CD的位置关系, 画出图形并直接写出你的结论;
(2)若AD=6,tanB=
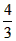 ,AE=1,在①的条件下,设CP1=x,
,AE=1,在①的条件下,设CP1=x,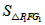 =y,求y与x之间的函数关系式,并写出自变量x的取值范围。
=y,求y与x之间的函数关系式,并写出自变量x的取值范围。 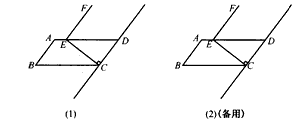
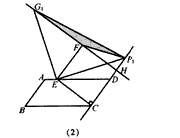
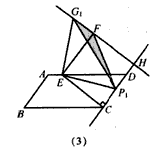
| 解:(l)①直线FG1与直线CD的位置关系为互相垂直,证明:如图(1), 设直线FG1与直线CD的交点为H, ∵线段EC、EP1分别绕点E逆时针旋转90°依次得到线段EF、EG1, ∴∠P1EG1=∠CEF=90°,EG1=EP1,EF=EC, ∵∠G1EF=90°-∠P1EF ∠P1EC=90°-∠P1EF, ∴∠G1EF=∠P1EC, ∴△G1EF≌△P1EC, ∴∠G1FE=∠P1CE, ∵EC⊥CD, ∴∠ P1CE=90°, ∴∠G1FE=90°, ∴∠EFH=90°, ∴∠FHC=90°, ∴FG1⊥CD, ②按题目要求所画图形见图(1),直线G1G2与直线CD的位置关系为互相垂直。 |
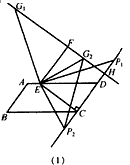 |
| (2)∵四边形ABCD是平行四边形, ∴∠B=∠ADC, ∵AD=6,AE=1,tanB= 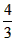 , , ∴DE=5,tan∠EDC=tanB= 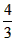 , ,可得CE=4, 由(1)可得四边形FECH为正方形, ①如图(2)当P1点在线段CH的延长线上时, ∵FG1=CP1=x,P1H=x-4, ∴ 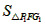 = =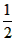 ×FG1×P1H= ×FG1×P1H=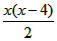 ∴y= 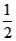 x2-2x(x>4), x2-2x(x>4),②如图(3),当P,点在线段CH上(不与C、H 两点重合)时, ∴FG1=CP1=x,P1H=4-x, ∴ 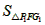 = =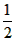 ×FG1×P1H= ×FG1×P1H=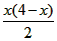 ∴y=- 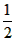 x2+2x(0 <x<4), x2+2x(0 <x<4),③当P1点与H点重合时,即x=4时,△P1FG1不存在, 综上所述,y与x之间的函数关系式及自变量x的取值范围是y= 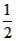 x2-2x(x >4)或y=- x2-2x(x >4)或y=-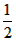 x2+2x(0<x<4)。 x2+2x(0<x<4)。 |
  |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 90°得到线段EG2.判断直线G1G2与直线CD的位置关系,画出图形并直接写出你的结论.
90°得到线段EG2.判断直线G1G2与直线CD的位置关系,画出图形并直接写出你的结论. 如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C. 如图,在?ABCD中,过点B的直线与对角线AC,边AD分别交于点E和点F,过点E作EG∥BC,交AB于G,则图中相似的三角形有
如图,在?ABCD中,过点B的直线与对角线AC,边AD分别交于点E和点F,过点E作EG∥BC,交AB于G,则图中相似的三角形有