Question

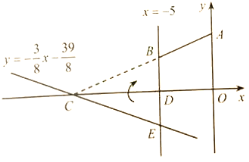
【题目】如图，直角坐标系中，，直线与轴交于点，直线与轴及直线分别交于点，．点，关于轴对称，连接．

(1)求点，的坐标及直线的解析式；

(2)设面积的和，求的值；

(3)在求(2)中时，嘉琪有个想法：“将沿轴翻折到的位置，而与四边形拼接后可看成，这样求便转化为直接求的面积不更快捷吗？”但大家经反复验算，发现，请通过计算解释他的想法错在哪里．

Answer 1

【答案】(1)C(-13，0)，E(-5，-3)，；(2)32；(3)见解析.

【解析】

试题分析：(1)由与x轴和直线x=-5的交点求得点C，E的坐标，点B，E关于x轴对称，求得B的坐标，由待定系数法求直线AB的解析式；(2)分别求△CDE的面积和梯形ABDO的面积；(3)点C不在直线AB上.

试题解析：(1)把y=0代入，解得x=-13，∴C(-13，0).

把x=-5代入，解得y=-3，∴E(-5，-3).

∵点B，E关于x轴对称，∴B(-5，3).

设直线AB的解析式为y=kx+b，则解得

∴直线AB的解析式为.

(2)∵CD=8，DE=DB=3，OA=OD=5，

∴,,即S=32.

(3)当x=-13时，=-0.2≠0.

∴点C不在直线AB上，即A，B，C三点不共线.

∴他的想法错在将△CDB与四边形ABDO拼接后看成了△AOC.