Question

【题目】如图，在△ABC中，AB＝AC＝5，BC＝8，点D是边BC上(不与B，C重合)一动点，∠ADE＝∠B＝，DE交AC于点E，若△DCE为直角三角形，则BD的值为_______.

Answer 1

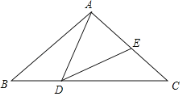
【答案】4或6.25

【解析】

因为∠C为定角，D、E为动点，所以△DCE为直角三角形有两种情况：

①当∠DEC=90°时，△DCE为直角三角形，如图1，证明∠ADC=∠AED=90°，根据等腰三角形三线合一的性质可求出BD的长；

②当∠EDC=90°时，△DCE为直角三角形，如图2，作辅助线，证明△BFA∽△BAD，根据相似三角形的性质可求出BD的长．

分两种情况：

①∠DEC=90°时，△DCE为直角三角形，如图1，

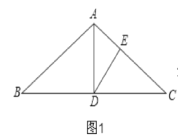
∴∠AED=90°，

∵AB=AC，

∴∠B=∠C，

∵∠ADE=∠B，

∴∠ADE=∠C，

∵∠DAE=∠DAC，

∴△ADE∽△ACD，

∴∠ADC=∠AED=90°，

∴AD⊥BC，

∴BD=BC=×8=4；

②当∠EDC=90°时，△DCE为直角三角形，如图2，

过A作AF⊥BC于F，则BF=4，

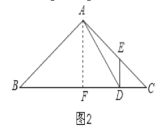
∵∠ADE+∠EDC=∠B+∠BAD，∠ADE=∠B，

∴∠EDC=∠BAD=90°，

∴∠BAD=∠BFA=90°，

∵∠B=∠B，

∴△BFA∽△BAD，

∴，

∵AB=5，

∴，

∴BD=6.25，

综上所述，BD为4或6.25，

故答案为：4或6.25.