题目内容
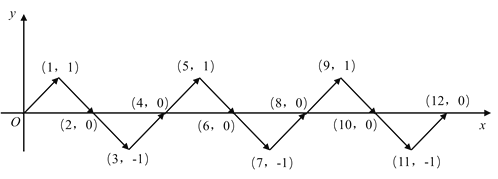
【题目】如图,动点![]() 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点
在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点![]() ,第2次运动到点
,第2次运动到点![]() ,第3次运动到点
,第3次运动到点![]() ,.….按照这样的运动规律,点
,.….按照这样的运动规律,点![]() 第17次运动到点( )
第17次运动到点( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
令P点第n次运动到的点为Pn点(n为自然数).列出部分Pn点的坐标,根据点的坐标变化找出规律“P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1)”,根据该规律即可得出结论.
令P点第n次运动到的点为Pn点(n为自然数).
观察,发现规律:P0(0,0),P1(1,1),P2(2,0),P3(3,-1),P4(4,0),P5(5,1),…,
∴P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1).
∵17=4×4+1,
∴P第17次运动到点(17,1).
故选:A.

练习册系列答案
相关题目