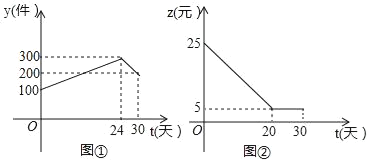
题目内容
【题目】如图,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,且
,且![]() ,设
,设![]() .
.
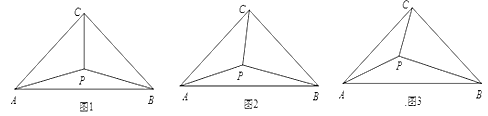
(1)如图1,若![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连结
,连结![]() ,易证
,易证![]() 为等边三角形,则
为等边三角形,则![]() ,
,![]() ;
;
(2)如图2,若![]() ,则
,则![]() ,
,![]() ;
;
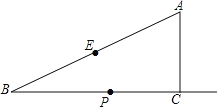
(3)如图3,试猜想![]() 和
和![]() 之间的数量关系,并给予证明.
之间的数量关系,并给予证明.
【答案】(1)![]() ,
,![]() (2)
(2)![]() ,
,![]() (3)
(3)![]()
【解析】
(1)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,只要证明△DAP为等边三角形,即可解决问题;
(2)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,只要证明△DAP为等腰直角三角形,即可解决问题;
(3)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,只要证明△BPA≌△BPD(SSS),即可解决问题;
解:(1)如图1中,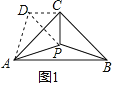
由旋转不变性可知:![]() ,
,![]() ,
,![]() ,
,
∵在等腰![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,CP为三线合一的线
,CP为三线合一的线
∴![]() ,
,![]()
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∴![]() ,
,
∴△APD是等边三角形,
∴∠ADP=∠APD=60°,
∵∠CDP=∠CPD=45°,
∴∠ADC=∠APC=∠CPB=105°,
∴∠APB=360°-105°-105°=150°,
∴α=150°,β=105°,
故答案为150°,105°.
(2)将△PBC绕点C顺时针旋转90°至△DAC,连结DP.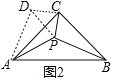
由旋转不变性可知:BP=AD,CD=CP,∠DCP=90°,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴△ADP是等腰直角三角形,
∴∠APD=90°,∠ADP=45°,
∴∠APC=135°,∠BPC=∠ADC=90°,
∴∠APB=360°-135°-90°=135°,
∴α=135°,β=90°,
故答案为135°,90°.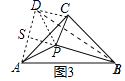
(3)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,延长PB交AD与S,
由旋转不变性可知:BP=AD,CD=CP,∠DCP=90°,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∵![]() ,
,
∴PA=PD,
∵∠BPC+∠CPS=180°,∠BPC=∠ADC,
∴∠ADC+∠CPS=180°,
∴∠PSD+∠PCD=180°,
∴∠PSD=90°,
∴PS⊥AD,
∵PA=PD,
∴△ADP是等腰直角三角形,
∴SA=SD,
∴△ABP是等腰直角三角形,
∴BA=BD,
∵BP=BP,PA=PD,BA=BD,
∴△BPA≌△BPD(SSS),
∴∠APB=∠BPD,
∴![]() ∠BPD-∠BPC=∠CPD=45°,
∠BPD-∠BPC=∠CPD=45°,
即:![]() .
.