Question

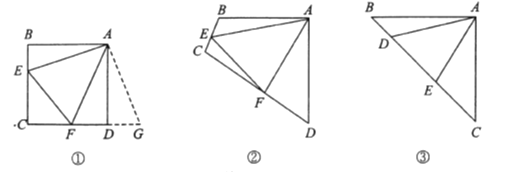
【题目】如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△ACD，连接AD,BC．若∠ACB=30°，AB=1，CC=x，则下列结论：①△AAD≌△CCB；②当x=1时，四边形ABCD是菱形；③当x=2时，△BDD为等边三角形.其中正确的是_______（填序号）．

Answer 1

【答案】①②③

【解析】①∵四边形ABCD是矩形，△A1C1D1由△ACD平移得到，
∴A1D1=AD=CB，AA1=CC1，A1D1∥AD∥BC，
∴∠ D1A1C1=∠BCA，
∴△ AAD≌△CCB.
②∵四边形ABCD是矩形，△A1C1D1是由△ACD平移得到，
∴C1D1=CD=AB，C1D1∥DC∥AB，
∴四边形ABC1D1是平行四边形，
在Rt△ABC中，点C1是线段AC的中点，
∴BC=AC,
而∠ACB=30°，
∴AB=AC,
∴AB=BC1，
∴四边形ABC1D1是菱形.

③x=2时，ABD1共线，且AD1=4，BD=4，DD1=4，

∴△BDD1为等边三角形.

所以①②③正确.