Question

【题目】如图，已知A（3，1），B（-2，3），线段AB与y轴相交于点C．

（1）求△AOB的面积；

（2）求点C的坐标；

（3）请直接写出直线AB与x轴的交点坐标．

Answer 1

【答案】（1）S△AOB=；（2）C（0，）；（3）直线AB与x轴交点为（，0）；

【解析】

（1）过A作AE⊥x轴于E，过B作BF⊥x轴于F，S△AOB=S梯形AEFB-S△AOE-S△FOB=--=；

（2）S△AOB=S△AOC+S△COB，则有=OB×3+，即可求OC；

（3）设直线AB的解析式y=kx+b，将A（3，1），B（-2，3）代入，即可得y=-x+；

解：（1）过A作AE⊥x轴于E，过B作BF⊥x轴于F，

，

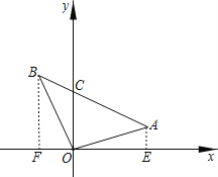
∵A（3，1），B（-2，3），

∴AE=1，BF=OE=3，FO=2，

∴EF=5，

∴S△AOB=S梯形AEFB-S△AOE-S△FOB=--=；

（2）∵S△AOB=S△AOC+S△COB，

∴=OB×3+，

∴OC=，

∴C（0，）；

（3）设直线AB的解析式y=kx+b，

将A（3，1），B（-2，3）代入，

∴，

∴，

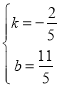∴y=-x+，

∴直线AB与x轴交点为（，0）；