题目内容
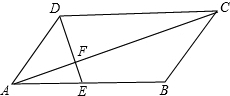平行四边形ABCD中，AE：EB=1：2，那么△AEF的周长与△CDF的周长之比为________．
1：3
分析：根据两对应角相等，两三角形是相似三角形，可判断△AEF与△CDF是相似三角形，相似三角形的周长比等于相似比．
解答：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴∠EAF=∠DCF，∠AEF=∠CDF，
∴△AEF∽△CDF，
∴
=
=
．
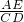故答案为：1：3．
点评：本题考查相似三角形的判定和性质以及平行四边形对边相等的性质，难度适中．
分析：根据两对应角相等，两三角形是相似三角形，可判断△AEF与△CDF是相似三角形，相似三角形的周长比等于相似比．
解答：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴∠EAF=∠DCF，∠AEF=∠CDF，
∴△AEF∽△CDF，
∴
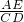==．故答案为：1：3．
点评：本题考查相似三角形的判定和性质以及平行四边形对边相等的性质，难度适中．
练习册系列答案
名校课堂系列答案
相关题目
如图，在平行四边形ABCD中，高h=4，则平行四边形ABCD的面积S=
如图，在平行四边形ABCD中，AE：EB=1：2，S△AEF=3，则S△FCD=
如图，在平行四边形ABCD中，E是BD上一点，AE的延长线交DC于点F，交BC的延长线于点G．求证：
如图，在平行四边形ABCD中，E、F分别是AD、BC的中点，AC分别交BE、DF于G、H，下列结论：
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．