题目内容
3.解方程:(1)(x-2)(x-5)=-2
(2)$\frac{7}{x+1}$+$\frac{3}{x-1}$=$\frac{10}{x}$.
分析 (1)先把方程化为一般式,然后利用因式分解法解方程;
(2)先把方程化为7x(x-1)+3x( x+1)=10(x+1)(x-1),然后解此整式方程,再进行检验确定原方程的解.
解答 解:(1)x2-7x+12=0,
(x-3)(x-4)=0,
x-3=0或x-4=0,
所以x1=3,x2=4;
(2)去分母得7x(x-1)+3x( x+1)=10(x+1)(x-1),
解得x=$\frac{5}{2}$,
经检验,x=$\frac{5}{2}$为原方程的解.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了解分式方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列由左到右的变形中,属于因式分解的是( )
| A. | x2-4x+4=x(x-4)+4 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x+9)(x-9)=x2-81 | D. | x2-2x-3=(x-3)(x+1) |
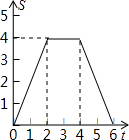
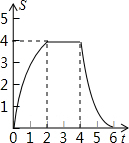
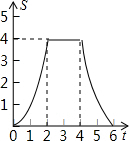
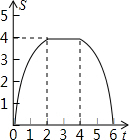
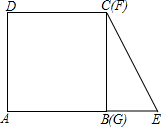 如图,边长为4的正方形ABCD的边BC与直角边分别是2和4的Rt△GEF的边GF重合,正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )
如图,边长为4的正方形ABCD的边BC与直角边分别是2和4的Rt△GEF的边GF重合,正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )