题目内容
如图,在等腰Rt△ABC中,AC=BC,∠ABC的平分线BE交AB边上的中线CD于点H,交AC于点E,延长BC到点F,使CF=CE,连接AF交BE的延长线于点G,连接GD.下列结论:①∠F=60°;②GD∥CB;③GH=HB;④∠CEH=∠CHE;⑤S△BCE:S△BEA=1:
 .
.
其中正确的结论有
- A.①③
- B.②④
- C.①③⑤
- D.②④⑤
D
分析:①证明△ACF≌△BCE,得∠F=∠BEC=67.5°;
②证明BG⊥AF,从而证明G为AF的中点,根据三角形中位线定理得GD∥CB;
③根据直角三角形斜边上中线等于斜边的一半得GD=BD.因CD不与GB垂直,故GH≠HB;
④∠CEH=∠CHE=67.5°;
⑤AB= BC.根据角平分线的性质判断.
BC.根据角平分线的性质判断.
解答:在△ACF和△BCE中,
∵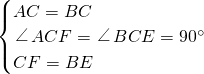 ,
,
∴△ACF≌△BCE.
①∠F=∠BEC=90°-22.5°=67.5°.故错误;
②∵∠F=67.5°,∠FBG=22.5°,
∴∠FGB=90°,即BG⊥AF.
∵BG平分角FBA,
∴△ABG≌△FBG.
∴AG=FG.
又D为AB中点,
∴GD∥CB.故正确;
③∵GD= AB=DB,
AB=DB,
∴△GDB为等腰三角形.
∵CD⊥AB,不与GB垂直,
∴GH≠HB.故错误;
④∠CEH=90°-22.5°=67.5°,
∠CHE=45°+22.5°=67.5°,
∴∠CEH=∠CHE.故正确;
⑤∵在等腰Rt△ABC中,AC=BC,
∴AB= BC.
BC.
∵BE平分∠ABC,
∴BC:BA=CE:EA=S△BCE:S△ABE=1: .
.
故正确.
故选D.
点评:此题考查全等三角形的判定与性质及三角形中位线定理、三角形角的角平分线性质等知识点,综合性较强.
分析:①证明△ACF≌△BCE,得∠F=∠BEC=67.5°;
②证明BG⊥AF,从而证明G为AF的中点,根据三角形中位线定理得GD∥CB;
③根据直角三角形斜边上中线等于斜边的一半得GD=BD.因CD不与GB垂直,故GH≠HB;
④∠CEH=∠CHE=67.5°;
⑤AB=
 BC.根据角平分线的性质判断.
BC.根据角平分线的性质判断.解答:在△ACF和△BCE中,
∵
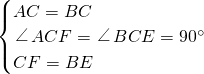 ,
,∴△ACF≌△BCE.
①∠F=∠BEC=90°-22.5°=67.5°.故错误;
②∵∠F=67.5°,∠FBG=22.5°,
∴∠FGB=90°,即BG⊥AF.
∵BG平分角FBA,
∴△ABG≌△FBG.
∴AG=FG.
又D为AB中点,
∴GD∥CB.故正确;
③∵GD=
 AB=DB,
AB=DB,∴△GDB为等腰三角形.
∵CD⊥AB,不与GB垂直,
∴GH≠HB.故错误;
④∠CEH=90°-22.5°=67.5°,
∠CHE=45°+22.5°=67.5°,
∴∠CEH=∠CHE.故正确;
⑤∵在等腰Rt△ABC中,AC=BC,
∴AB=
 BC.
BC.∵BE平分∠ABC,
∴BC:BA=CE:EA=S△BCE:S△ABE=1:
 .
.故正确.
故选D.
点评:此题考查全等三角形的判定与性质及三角形中位线定理、三角形角的角平分线性质等知识点,综合性较强.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
| A、①②③ | B、①④⑤ | C、①③④ | D、③④⑤ |
 上运动,且保持AD=CE.连接DE、DF、EF.
上运动,且保持AD=CE.连接DE、DF、EF. 如图,在等腰Rt△ABC中,∠C=90°,∠CBD=30°,则
如图,在等腰Rt△ABC中,∠C=90°,∠CBD=30°,则 如图,在等腰Rt△ABC中,∠ACB=90°,CA=CB,点M、N是AB上任意两点,且∠MCN=45°,点T为AB的中点.以下结论:①AB=
如图,在等腰Rt△ABC中,∠ACB=90°,CA=CB,点M、N是AB上任意两点,且∠MCN=45°,点T为AB的中点.以下结论:①AB= 如图,在等腰Rt△ABC中,∠C=90°,AC=8
如图,在等腰Rt△ABC中,∠C=90°,AC=8