题目内容
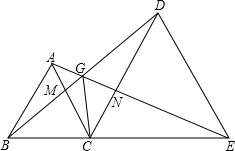 如图,△ABC与△CDE均为等边三角形,B、C、E在同一直线上,AE、BD交于点G,AC交BD于M,CD交AE于N,连接CG.
如图,△ABC与△CDE均为等边三角形,B、C、E在同一直线上,AE、BD交于点G,AC交BD于M,CD交AE于N,连接CG.
(1)若AB=2,DE=5,求AE的长.
(2)求证:EG=CG+DG.
(1)解:过A作AP⊥BE于P,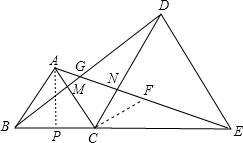
在等边三角形△ABC中,BC=2,
∴CP= BC=1,PA=
BC=1,PA=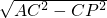 =
= =
= ,
,
∵CE=5,
∴PE=CP+CE=6,
在Rt△APE中,AE=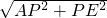 =
=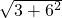 =
= ,
,
(2)证明:在EG上截取FE=DG,连接CF,CG,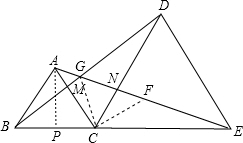
在等边△ABC和等边△DCE中,
AC=BC,CE=CD,∠DCE=∠BCA=60°,
∴∠DCE+∠DCM=∠BCA+∠DCM,
即∠ACE=∠BCD,
在△ACE和△BCD中,

∴△ACE≌△BCD(SAS),
∴∠BDC=∠AEC,
在△DGC和△EFC中,
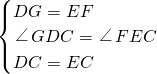
∴△DGC≌△EFC(SAS),
∴CG=CF,∠GCD=∠FCE,
∵∠FCE+∠FCD=60°,
∴∠GCD+∠FCD=60°,即∠GCF=60°
∴△GCF为等边三角形,
∴CG=GF,
∴GE=GF+FE=GD+CG,
即EG=CG+DG.
分析:(1)过A作AP⊥BE于P,求出CP,求出PE,根据勾股定理求出AE即可.
(2)证△ACE≌△BCD,推出△ACE≌△BCD,推出∠BDC=∠AEC,证△DGC≌△EFC,推出CG=CF,∠GCD=∠FCE,得出等边三角形GCF,推出CG=GF即可.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定,勾股定理,等腰三角形的性质的应用,主要考查学生综合运用性质进行推理的能力.

在等边三角形△ABC中,BC=2,
∴CP=
 BC=1,PA=
BC=1,PA=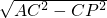 =
= =
= ,
,∵CE=5,
∴PE=CP+CE=6,
在Rt△APE中,AE=
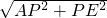 =
=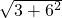 =
= ,
,(2)证明:在EG上截取FE=DG,连接CF,CG,

在等边△ABC和等边△DCE中,
AC=BC,CE=CD,∠DCE=∠BCA=60°,
∴∠DCE+∠DCM=∠BCA+∠DCM,
即∠ACE=∠BCD,
在△ACE和△BCD中,

∴△ACE≌△BCD(SAS),
∴∠BDC=∠AEC,
在△DGC和△EFC中,
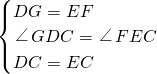
∴△DGC≌△EFC(SAS),
∴CG=CF,∠GCD=∠FCE,
∵∠FCE+∠FCD=60°,
∴∠GCD+∠FCD=60°,即∠GCF=60°
∴△GCF为等边三角形,
∴CG=GF,
∴GE=GF+FE=GD+CG,
即EG=CG+DG.
分析:(1)过A作AP⊥BE于P,求出CP,求出PE,根据勾股定理求出AE即可.
(2)证△ACE≌△BCD,推出△ACE≌△BCD,推出∠BDC=∠AEC,证△DGC≌△EFC,推出CG=CF,∠GCD=∠FCE,得出等边三角形GCF,推出CG=GF即可.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定,勾股定理,等腰三角形的性质的应用,主要考查学生综合运用性质进行推理的能力.

练习册系列答案
相关题目
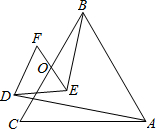 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )A、
| ||
B、
| ||
| C、5:3 | ||
| D、不确定 |
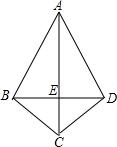 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.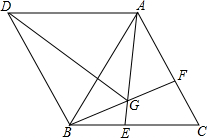 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G. 29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.
29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.