题目内容
 如图,⊙O的直径为10cm,弦AB为8cm,P是弦AB上一点,若OP的长为整数,则满足条件的点P有
如图,⊙O的直径为10cm,弦AB为8cm,P是弦AB上一点,若OP的长为整数,则满足条件的点P有
- A.2个
- B.3个
- C.4个
- D.5个
D
分析:如图,⊙O的直径为10cm,弦AB为8cm,当OP⊥AB时OP有最小值,连接OA,过O作OD⊥AB,根据垂径定理和勾股定理即可求出OD为3,
所以得到当OP⊥AB时P的最小值为3,当OP与OA重合时P最大为5,这样就可以判定P在AD之间和在BD之间的整数点,然后即可得到结论.
解答: 解:如图,连接OA,过O作OD⊥AB于D,
解:如图,连接OA,过O作OD⊥AB于D,
∵⊙O的直径为10cm,弦AB为8cm,
当OP⊥AB时OP有最小值,
则AD= AB=4cm,
AB=4cm,
由勾股定理得OD= =
= =3cm,
=3cm,
∴当OP⊥AB时OP的最小值为3,
当OP与OA重合时P最大为5,
∴P在AD中间有3,4,5三个整数点,
在BD之间有4,5,两个整数点,
故P在AB上有5个整数点.
故选D.
点评:此题属简单题目,涉及到垂径定理及勾股定理的运用,要求学生仔细阅读题目,充分理解题意,细心解答.
分析:如图,⊙O的直径为10cm,弦AB为8cm,当OP⊥AB时OP有最小值,连接OA,过O作OD⊥AB,根据垂径定理和勾股定理即可求出OD为3,
所以得到当OP⊥AB时P的最小值为3,当OP与OA重合时P最大为5,这样就可以判定P在AD之间和在BD之间的整数点,然后即可得到结论.
解答:
 解:如图,连接OA,过O作OD⊥AB于D,
解:如图,连接OA,过O作OD⊥AB于D,∵⊙O的直径为10cm,弦AB为8cm,
当OP⊥AB时OP有最小值,
则AD=
 AB=4cm,
AB=4cm,由勾股定理得OD=
 =
= =3cm,
=3cm,∴当OP⊥AB时OP的最小值为3,
当OP与OA重合时P最大为5,
∴P在AD中间有3,4,5三个整数点,
在BD之间有4,5,两个整数点,
故P在AB上有5个整数点.
故选D.
点评:此题属简单题目,涉及到垂径定理及勾股定理的运用,要求学生仔细阅读题目,充分理解题意,细心解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
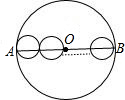 如图,⊙O的直径为AB,周长为P1,在⊙O内的n个圆心在AB上且依次相外切的等圆,且其中左、右两侧的等圆分别与⊙O内切于A、B,若这n个等圆的周长之和为P2,则P1和P2的大小关系是( )
如图,⊙O的直径为AB,周长为P1,在⊙O内的n个圆心在AB上且依次相外切的等圆,且其中左、右两侧的等圆分别与⊙O内切于A、B,若这n个等圆的周长之和为P2,则P1和P2的大小关系是( )| A、P1<P2 | B、P1=P2 | C、P1>P2 | D、不能确定 |
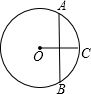 如图,⊙O的直径为10 cm,弦AB垂直平分半径OC,则弦AB长为( )
如图,⊙O的直径为10 cm,弦AB垂直平分半径OC,则弦AB长为( )| A、2.5cm | ||
| B、5cm | ||
C、5
| ||
| D、10cm |
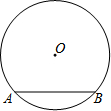 (2013•南京二模)如图,⊙O的直径为10,弦AB的长为8,则点O到AB的距离为
(2013•南京二模)如图,⊙O的直径为10,弦AB的长为8,则点O到AB的距离为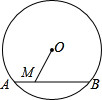 如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是
如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是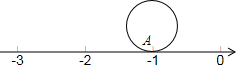 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是
如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是