题目内容
在三角形ABC中，若∠A+∠B=120°，则sinC等于
- A.
- B.
- C.
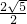
- D.
B
分析：根据三角形内角和180°得出∠C的值，再代入sinC中求解．
解答：∵三角形ABC中，∠A+∠B=120°，
∴∠C=180°-120°=60°，
∴sinC=sin60°=．
故选B．
点评：本题考查特殊角的三角函数值及三角形内角和定理．
分析：根据三角形内角和180°得出∠C的值，再代入sinC中求解．
解答：∵三角形ABC中，∠A+∠B=120°，
∴∠C=180°-120°=60°，
∴sinC=sin60°=
．故选B．
点评：本题考查特殊角的三角函数值及三角形内角和定理．
练习册系列答案
相关题目
在三角形ABC中，若∠A+∠B=120°，则sinC等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，已知在三角形ABC中，若AB=AC，BD=BC，∠C=70°，求∠ABD的度数=
如图，在三角形ABC中，若AB=AC，BD=BC，若∠ABD=30°，则∠A的大小是
如图，已知在三角形ABC中，若AB=AC，BD=BC，∠C=70°，求∠ABD的度数=________．