题目内容
【题目】如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.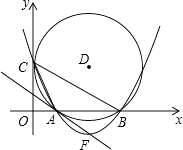
(1)则D点的坐标是 ( , ),圆的半径为;
(2)sin∠ACB=;经过C、A、B三点的抛物线的解析式;
(3)设抛物线的顶点为F,证明直线FA与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大值是多少,并求出N点坐标.
【答案】
(1)5;4;5
(2)![]() ;y=
;y= ![]() x2﹣
x2﹣ ![]() x+4
x+4
(3)
证明:因为D为圆心,A在圆周上,DA=r=5,故只需证明∠DAF=90°,
抛物线顶点坐标:F(5,﹣ ![]() ),DF=4+
),DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() ,
,
∵DA2+AF2=52+( ![]() )2=
)2= ![]() =(
=( ![]() )2=DF2,
)2=DF2,
∴∠DAF=90°
所以AF切于圆D
(4)
解:存在点N,使△CBN面积最大.
根据点B及点C的坐标可得:直线BC的解析式为:y=﹣ ![]() x+4,
x+4,
设N点坐标(a, ![]() ),过点N作NP与y轴平行,交BC于点P,
),过点N作NP与y轴平行,交BC于点P,
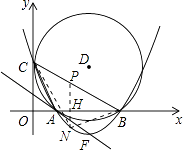
可得P点坐标为(a, ![]() ),
),
则NP= ![]() ﹣(
﹣( ![]() )=
)= ![]()
故S△BCN=S△BPN+S△PCN= ![]() ×PN×OH+
×PN×OH+ ![]() ×PN×BH=
×PN×BH= ![]() PN×BO=
PN×BO= ![]() ×8×(
×8×( ![]() )=16﹣(a﹣4)2
)=16﹣(a﹣4)2
当a=4时,S△BCN最大,最大值为16,此时,N(4,﹣2)
【解析】(1)解:连接DC,则DC⊥y轴,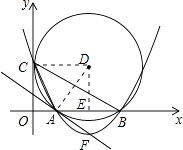
过点D作DE⊥AB于点E,则DE垂直平分AB,
∵AB=6,
∴AE=3,
在Rt△ADE中,AD= ![]() =
= ![]() =5,
=5,
故可得点D的坐标为(5,4),圆的半径为5;
·(2)解:在Rt△AOC中,AC= ![]() =
= ![]() =2
=2 ![]() ,
,
在Rt△BOC中,BC= ![]() =
= ![]() =4
=4 ![]() ,
,
∵S△ABC= ![]() AC×BCsin∠ACB=
AC×BCsin∠ACB= ![]() AB×CO,
AB×CO,
∴sin∠ACB= ![]() =
= ![]() ;
;
设经过点A、B、C三点的抛物线解析式为:y=ax2+bx+c,
将三点坐标代入可得: 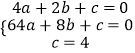 ,
,
解得: 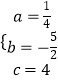 ,
,
故经过C、A、B三点的抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x+4.
x+4.