题目内容
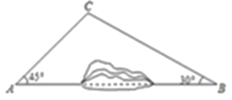
【题目】已知在![]() 中,∠C=90°,AC=8,BC=6,
中,∠C=90°,AC=8,BC=6,
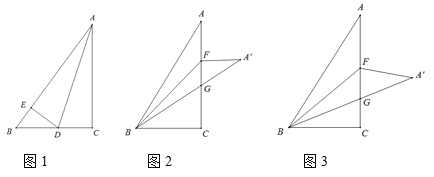
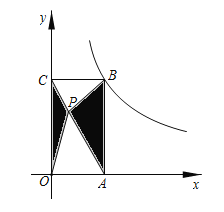
(1)若AD是∠BAC的角平分线,AD交BC边于D,过点D作DE⊥AB与点E(如图1),请求出BE的长及![]() 的值;
的值;
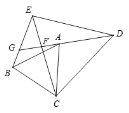
(2)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若BC=CF,如图2,请证明
与AC交于点G,若BC=CF,如图2,请证明![]() ∽
∽![]() ;
;
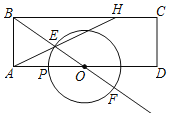
(3)点F是边AC上的一点,连接BF,把![]() 沿着直线BF对折得到
沿着直线BF对折得到![]() ,
,![]() 与AC交于点G,若
与AC交于点G,若![]() ,如图3,请求出
,如图3,请求出![]() 的值(可以直接利用第(1)题求出的结论)
的值(可以直接利用第(1)题求出的结论)
【答案】(1)![]() ;
; ![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)设CD=DE=x,则BD=6-x,通过![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,证明△ADE≌△ADC(AAS),可得CD=DE,AE=AC=8,推出
,证明△ADE≌△ADC(AAS),可得CD=DE,AE=AC=8,推出![]() ,再根据勾股定理构建方程即可解决问题.
,再根据勾股定理构建方程即可解决问题.
(2)设![]() 的度数为
的度数为![]() ,由折叠可得
,由折叠可得![]() ,根据
,根据![]() ,
,![]() ,
,
可得![]() ,利用折叠和三角形的外角的性质,可得
,利用折叠和三角形的外角的性质,可得![]() ,则可证
,则可证![]() ∽
∽![]()
(3)作A′H⊥AC于H,设![]() 的长度为
的长度为![]() ,利用
,利用![]() ≌
≌![]() ,
,![]() ∥
∥![]() ,得到
,得到![]() ,由(1)得
,由(1)得![]() ,则
,则![]() ,解得
,解得![]() ,则有
,则有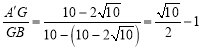 .
.
解:∵∠C=90°,AC=8,BC=6,
∴AB=10,
(1)设![]() 的长度为
的长度为![]() ,则
,则![]()
∵![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]()
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (AAS)
(AAS)
∴![]()
∴![]()
在直角![]() 中,
中,![]()
∴![]()
解得![]()
∴![]()
综上所述,![]() ,
,![]()
(2)设![]() 的度数为
的度数为![]() ,由折叠可得
,由折叠可得![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]() ∽
∽![]()
(3)如图,过点![]() 作
作![]() 交
交![]() 于
于![]() 点,
点,
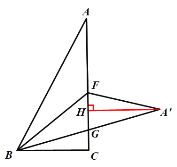
设![]() 的长度为
的长度为![]() ,由折叠可得
,由折叠可得![]() ≌
≌![]()
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]() ∥
∥![]()
∴![]()
由(1)得![]()
∴![]()
∴![]()
解得![]()
∴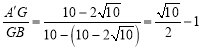

 应用题作业本系列答案
应用题作业本系列答案【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。