题目内容
(本题10分)已知:抛物线 以点C为顶点且过点B,抛物线
以点C为顶点且过点B,抛物线 以点B为顶点且过点C,分别过点B、C作
以点B为顶点且过点C,分别过点B、C作 轴的平行线,交抛物线
轴的平行线,交抛物线 、
、 于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.
于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.

(1)如图1,①求证四边形ECFB为正方形;②求点A的坐标;

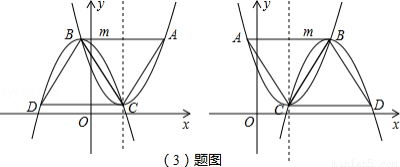
(2)①如图2,若将抛物线“ ”改为“
”改为“ ”,其他条件不变,求CD的长;
”,其他条件不变,求CD的长;

②如图3,若将抛物线“ ”改为“
”改为“ ”,其他条件不变,求
”,其他条件不变,求 的值;
的值;

(3)若将抛物线“ ”改为抛物线“
”改为抛物线“ ”,其他条件不变,请用含b2的
”,其他条件不变,请用含b2的
代数式表示b1.
(1)①详见解析;② A(-1,1);(2)①2;② 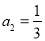 ;(3)
;(3)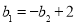 或
或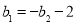
【解析】
试题分析:(1)①由于AB∥x轴,显然点A、B关于抛物线y1=x2的对称轴对称,可得AC=BC,已知AB=AC,那么△ABC必为等边三角形;
②由抛物线y1的解析式设出点A的坐标,再根据△ABC是等边三角形列出点A横、纵坐标的关系式,以此确定点A的坐标.
(2)①若称AB与抛物线y1对称轴的交点为E,可设AE=BE=m(m>0),在等边△ABC中,CE=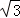 m,可用m表示出点B的坐标,代入抛物线解析式中即可求出m的值,则AB的长可求;在(1)的解答过程中,不难看出△ABC、△BCD都是等边三角形,因此由CD=BC=AB即可得解;
m,可用m表示出点B的坐标,代入抛物线解析式中即可求出m的值,则AB的长可求;在(1)的解答过程中,不难看出△ABC、△BCD都是等边三角形,因此由CD=BC=AB即可得解;
②将y1的解析式写成顶点式,即:y1=3(x﹣h)2+k,首先根据等边△ABC的特点表达出点B的坐标,将点B的坐标代入抛物线y1的解析式中,由此求得m的值;抛物线y2以点B为顶点,可先写成顶点式,再将点A的坐标代入其中来确定a2的值.
(3)由于这个小题并没有说明按给出的三个图求解,所以还需考虑抛物线y2在y1左侧的情况,但解法是相同的,仍以y2在y1右侧为例进行说明:
在(2)①的解答过程中,我们不难看出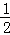 CD=
CD=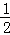 AB=m=
AB=m=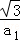 ,而
,而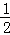 AB的长度正好是两个抛物线对称轴的差的绝对值,那么可以拿
AB的长度正好是两个抛物线对称轴的差的绝对值,那么可以拿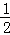 CD的长来作为等量关系列出关系式,据此求得b1、b2的关系式.
CD的长来作为等量关系列出关系式,据此求得b1、b2的关系式.
试题解析:(1)①∵AB∥x轴,∴A、B关于y轴对称,即AC=BC;
又∵AB=AC,∴AB=AC=BC;
即:△ABC是等边三角形.
②设点A的坐标为(x,x2)(x<0);
在等边△ABC中,x2=tan60°•(﹣x),解得:x1=0、x2=﹣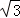
∴A(﹣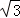 ,3).
,3).
(2)设线段AB交抛物线y1的对称轴于点E,AE=BE=m(m>0);
①如图(2)﹣①,在Rt△BCE中,BE=m,EC=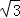 m,则B(m,
m,则B(m,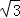 m+1);
m+1);
由于点B在y1=x2+1的函数图象上,所以有:
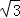 m+1=m2+1,解得:m=
m+1=m2+1,解得:m=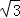
∴AB=2BE=2m=2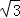 ;
;
同(1)①可知,△BCD、△ABC都是等边三角形,则CD=AB=2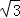 .
.
②设抛物线y1=3x2+b1x+c1=3(x﹣h)2+k,则C(h,k)、B(h+m,k+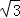 m);
m);
由于点B在y1=3(x﹣h)2+k上,有:
k+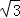 m=3m2+k,解得:m=
m=3m2+k,解得:m=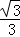
∴B(h+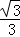 ,k+1);
,k+1);
则抛物线y2=a2(x﹣h﹣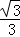 )2+k+1,代入C(h,k),得:
)2+k+1,代入C(h,k),得:
a2× +k+1=k,解得:a2=﹣3.
+k+1=k,解得:a2=﹣3.
(3)由(2)②知,a2=﹣a1;
由(2)①知,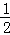 CD=
CD=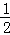 AB=m=|﹣
AB=m=|﹣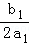 ﹣(﹣
﹣(﹣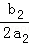 )|=|
)|=|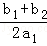 |,
|,
而m=|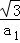 |(由(2)的解答过程可知),则:
|(由(2)的解答过程可知),则:
|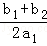 |=|
|=|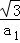 |,解得:b1+b2=±2
|,解得:b1+b2=±2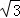 ;
;
即: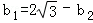 或
或 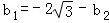 .
.
考点: 二次函数综合题





















