题目内容
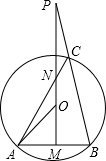 如图,O是△ABC的外心,弦AB的垂直平分线与AB和AC分别相交于点M、N,与BC边的延长线相交于点P,求证:OA2=ON•OP.
如图,O是△ABC的外心,弦AB的垂直平分线与AB和AC分别相交于点M、N,与BC边的延长线相交于点P,求证:OA2=ON•OP.
分析:连接OB,所求的乘积式可化为:OA•OB=ON•OP;将上式化为比例式,然后证线段所在的三角形相似,即证△OAN∽△OPB.
解答: 证明:连接OB;
证明:连接OB;
∵PM垂直平分AB,
∴OA=OB,AM=BM,OM⊥AB;
∴∠AOM=∠BOM=
∠AOB;
∵∠ACB=
∠AOB,∴∠ACB=∠AOM;
∴∠NAO+∠ANO=∠P+∠PNC;
∵∠PNC=∠ANO,∴∠P=∠NAO;
∵∠AOM=∠MOB,
∴∠AON=∠BOP;
∴△ANO∽△PBO,
∴
=
,即OA•OB=OP•ON;
∵OA=OB,
∴OA2=ON•OP.
 证明:连接OB;
证明:连接OB;∵PM垂直平分AB,
∴OA=OB,AM=BM,OM⊥AB;
∴∠AOM=∠BOM=
| 1 |
| 2 |
∵∠ACB=
| 1 |
| 2 |
∴∠NAO+∠ANO=∠P+∠PNC;
∵∠PNC=∠ANO,∴∠P=∠NAO;
∵∠AOM=∠MOB,
∴∠AON=∠BOP;
∴△ANO∽△PBO,
∴
| ON |
| OB |
| OA |
| OP |
∵OA=OB,
∴OA2=ON•OP.
点评:此题主要考查的是相似三角形的判定和性质,涉及到的知识点有:线段垂直平分线的性质、等腰三角形的性质、圆周角定理、三角形的外角性质等,综合性强,难度偏大.

练习册系列答案
相关题目
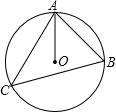 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
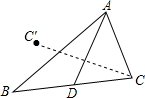 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=