题目内容
在等腰梯形ABCD中,AD=BC,∠A比∠C小50°,则梯形各内角中最小角的度数为________.
65°
分析:由在等腰梯形ABCD中,AD=BC,∠A比∠C小50°,可得∠A+∠A+50°=180°,继而求得答案.
解答: 解:∵在等腰梯形ABCD中,AD=BC,
解:∵在等腰梯形ABCD中,AD=BC,
∴∠A=∠B,∠B+∠C=180°,
∵∠A比∠C小50°,
∴∠A+∠A+50°=180°,
解得:∠A=65°,
∴∠B=∠A=65°,∠C=∠D=115°.
∴梯形各内角中最小角的度数为:65°.
故答案为:65°.
点评:此题考查了等腰梯形的性质.此题比较简单,注意掌握方程思想与数形结合思想的应用.
分析:由在等腰梯形ABCD中,AD=BC,∠A比∠C小50°,可得∠A+∠A+50°=180°,继而求得答案.
解答:
 解:∵在等腰梯形ABCD中,AD=BC,
解:∵在等腰梯形ABCD中,AD=BC,∴∠A=∠B,∠B+∠C=180°,
∵∠A比∠C小50°,
∴∠A+∠A+50°=180°,
解得:∠A=65°,
∴∠B=∠A=65°,∠C=∠D=115°.
∴梯形各内角中最小角的度数为:65°.
故答案为:65°.
点评:此题考查了等腰梯形的性质.此题比较简单,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.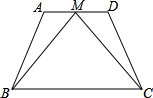 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.