题目内容
20.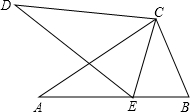 如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
分析 根据全等三角形对应角相等可得∠B=∠DEC,全等三角形对应边相等可得BC=EC,根据等边对等角可得∠B=∠BEC,从而得到∠BEC=∠DEC,再根据角平分线的定义证明即可.
解答 证明:∵△ABC≌△DEC,
∴∠B=∠DEC,BC=EC,
∴∠B=∠BEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
点评 本题考查了全等三角形的性质,等边对等角的性质,熟练掌握全等三角形的性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在平面直角坐标系中,把点P(-2,3)向右平移5个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
| A. | (3,-3) | B. | (-3,3) | C. | (3,3)或(-3,-3) | D. | (3,-3)或(-3,3) |
15.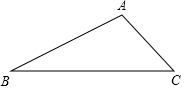 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
(1)用尺规作∠BAC的角平分线AE;
(2)用三角板作AC边上的高BD;
(3)用尺规作AC边上的垂直平分线MN.
 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)(1)用尺规作∠BAC的角平分线AE;
(2)用三角板作AC边上的高BD;
(3)用尺规作AC边上的垂直平分线MN.
9.下列各式结果为负数的是( )
| A. | -(-5) | B. | -|-3| | C. | (-2)6 | D. | |2-6| |
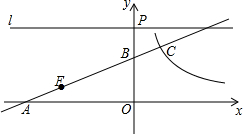 已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题:
已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题: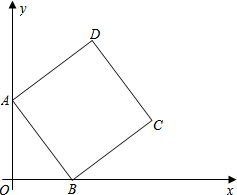 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长满足(x-$\frac{7}{2}$)2=$\frac{1}{4}$中的x.其中OA>OB.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长满足(x-$\frac{7}{2}$)2=$\frac{1}{4}$中的x.其中OA>OB.