题目内容
下列由三条线段a、b、c构成的三角形:①a=2mn,b=m2-n2,C=m2+n2(m>n>0),②a=2n+1,b=2n2+2n+1,c=2n2+2n(n>0),③a=3k,b=4k,c=5k(k>0),④
:
:
=1:
:2,其中能构成直角三角形的有( )
| a |
| b |
| c |
| 3 |
分析:判断一组数能否成为直角三角形的三边,就是看是否满足两较小边的平方和等于最大边的平方,将题目中的各题一一做出判断即可.
解答:解:①∵(m2-n2)2+(2mn)2=m4+n4-2m2n2+4m2n2=m4+n4+2m2n2=(m2+n2)2,
∴能成为直角三角形的三边长;
②∵(2n)2+(2n2+2n)2=(2n2+2n+1),
∴能成为直角三角形的三边长;
③(3k)2+(4k)2=(5k)2,
∴能成为直角三角形的三边长;
④∵(
)2+(
)2=(
)2,
∴能成为直角三角形的三边长;
∴中能构成直角三角形的有4组,
故选D.
∴能成为直角三角形的三边长;
②∵(2n)2+(2n2+2n)2=(2n2+2n+1),
∴能成为直角三角形的三边长;
③(3k)2+(4k)2=(5k)2,
∴能成为直角三角形的三边长;
④∵(
| a |
| b |
| c |
∴能成为直角三角形的三边长;
∴中能构成直角三角形的有4组,
故选D.
点评:本题考查了勾股定理的逆定理的应用,在应用时注意是两较短边的平方和等于最长边的平方.

练习册系列答案
相关题目

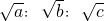 =1:
=1: :2,其中能构成直角三角形的有
:2,其中能构成直角三角形的有