题目内容
(2013•海淀区一模)如图1所示,圆上均匀分布着11个点A1,A2,A3,…,A11.从A1起每隔k个点顺次连接,当再次与点A1连接时,我们把所形成的图形称为“k+1阶正十一角星”,其中1≤k≤8(k为正整数).例如,图2是“2阶正十一角星”,那么∠A1+∠A2+…+∠A11=

1260°
1260°
;当∠A1+∠A2+…+∠A11=900°时,k=2或7
2或7
.
分析:根据题意先得出∠A1=7×
,从而得到∠A1+∠A2+…+∠A11的度数;分(9-2k)×
=2×
,
(2k-9)×
=2×
两种情况讨论可得当∠A1+∠A2+…+∠A11=900°时,k的值.
| 180° |
| 11 |
| 360° |
| 11 |
| 900° |
| 11 |
(2k-9)×
| 360° |
| 11 |
| 900° |
| 11 |
解答:解:看图2,设圆心为O,则优角A10OA3的度数为角A1的2倍.
而优角A10OA3=∠A10OA9+∠A9OA8+∠A8OA7+…+∠A4OA3,
而每个∠AkOAk-1=
,所以,优角A10OA3=7×
,
进而∠A1=优角A10OA3÷2=7×
,
所以∠A1+∠A2+…+∠A11=7×180°=1260°;
由题意,∠A1即为∠Ak+1A1A12-k,
当k<6时,同(1)问,可计算得那个优角的度数为(9-2k)×
,
因此,(9-2k)×
=2×
,
解得k=2,
当k>6时,优角的度数为(2k-9)×
,
因此(2k-9)×
=2×
解得k=7.
综上,k=2或7.
故答案为:1260°,2或7.
而优角A10OA3=∠A10OA9+∠A9OA8+∠A8OA7+…+∠A4OA3,
而每个∠AkOAk-1=
| 360° |
| 11 |
| 360° |
| 11 |
进而∠A1=优角A10OA3÷2=7×
| 180° |
| 11 |
所以∠A1+∠A2+…+∠A11=7×180°=1260°;
由题意,∠A1即为∠Ak+1A1A12-k,
当k<6时,同(1)问,可计算得那个优角的度数为(9-2k)×
| 360° |
| 11 |
因此,(9-2k)×
| 360° |
| 11 |
| 900° |
| 11 |
解得k=2,
当k>6时,优角的度数为(2k-9)×
| 360° |
| 11 |
因此(2k-9)×
| 360° |
| 11 |
| 900° |
| 11 |
解得k=7.
综上,k=2或7.
故答案为:1260°,2或7.
点评:考查了k+1阶正十一角星,关键是理解优角A10OA3的度数为角A1的2倍的知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
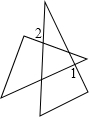 (2013•海淀区一模)一副三角板如图放置,若∠1=90°,则∠2的度数为( )
(2013•海淀区一模)一副三角板如图放置,若∠1=90°,则∠2的度数为( )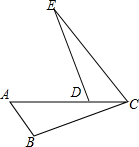 (2013•海淀区一模)已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.
(2013•海淀区一模)已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.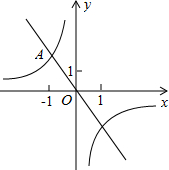 (2013•海淀区一模)如图,在平面直角坐标系xOy中,反比例函数
(2013•海淀区一模)如图,在平面直角坐标系xOy中,反比例函数