Question

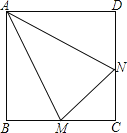
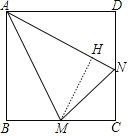
【题目】如图，M、N分别是正方形ABCD的边BC、CD上的点，已知：∠MAN＝30°，AM＝AN，△AMN的面积为1．

(1)求∠BAM的度数；

(2)求正方形ABCD的边长．

Answer 1

【答案】(1)∠BAM＝30°；(2)正方形ABCD的边长为．

【解析】

(1)只要证明△ABM≌△ADN(HL)，推出∠BAM＝∠DAN，由∠MAN＝30°，∠BAD＝90°，即可推出∠BAM＝30°；

(2)作MH⊥AN于H．设BM＝x，则AM＝AN＝2x，MH＝x，根据ANMH＝1，列出方程即可；

解：(1)∵四边形ABCD是正方形，

∴AB＝AD，∠B＝∠D＝∠BAD＝90°，

∵AM＝AN，

在Rt△ABM和Rt△ADN中，

，

∴△ABM≌△ADN(HL)，

∴∠BAM＝∠DAN，

∵∠MAN＝30°，∠BAD＝90°，

∴∠BAM＝30°．

(2)作MH⊥AN于H．设BM＝x，则AM＝AN＝2x，MH＝x，

∵ANMH＝1，

∴2xx＝1，

解得x＝1或﹣1(舍弃)，

∴AB＝BM＝，

∴正方形ABCD的边长为．