题目内容
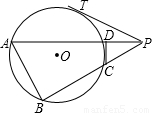
已知如图，⊙O的内接四边形ABCD，AD、BC的延长线交于P点，PT切⊙O于T点，PT=6，PC=4，AD=9，则BC=| CD | AB |
分析：根据切割线定理求得PB的长，进一步求得BC的长；再根据切割线定理求得PD的长，从而依据相似三角形的性质即可求得CD：AB的值．
解答：解：∵PT切⊙O于T点，PT=6，PC=4，AD=9，
∴PT2=PA•PD=PB•PC．
则PB=
=9，BC=5；
PD•（PD+9）=36，
PD=3．
∵∠P=∠P，∠PCD=∠A，
∴△PCD∽△PAB，
∴
=
=
．
∴PT2=PA•PD=PB•PC．
则PB=
| PT2 |
| PC |
PD•（PD+9）=36，
PD=3．
∵∠P=∠P，∠PCD=∠A，
∴△PCD∽△PAB，
∴
| CD |
| AB |
| PD |
| PB |
| 1 |
| 3 |
点评：此题综合运用了切割线定理、相似三角形的判定和性质．
练习册系列答案
互动课堂系列答案
相关题目
= ．
= ．
= ．
= ．
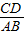
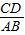