题目内容
如图：把两张宽度都为1的长方形纸条重叠在一起，则重叠部分（阴影部分）的面积为（ ）| A、1 | ||
| B、sinα | ||
C、
| ||
D、
|
分析：首先过A作AE⊥BC，AF⊥CD于F，垂足为E，F，证明△ABE≌△ADF，从而证明四边形ABCD是菱形，再利用三角函数算出BC的长，最后根据菱形的面积公式算出重叠部分的面积即可．
解答：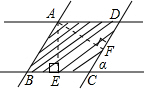
解：如右图所示：过A作AE⊥BC，AF⊥CD于F，垂足为E，F，
∴∠AEB=∠AFD=90°，
∵AD∥CB，AB∥CD，
∴四边形ABCD是平行四边形，
∵纸条宽度都为1，
∴AE=AF=1，
在△ABE和△ADF中，
，
∴△ABE≌△ADF（AAS），
∴AB=AD，
∴四边形ABCD是菱形．
∴BC=AB，
∵
=sinα，
∴BC=AB=
，
∴重叠部分（图中阴影部分）的面积为：BC×AE=1×
=
，
故选：C．
解：如右图所示：过A作AE⊥BC，AF⊥CD于F，垂足为E，F，∴∠AEB=∠AFD=90°，
∵AD∥CB，AB∥CD，
∴四边形ABCD是平行四边形，
∵纸条宽度都为1，
∴AE=AF=1，
在△ABE和△ADF中，
|
∴△ABE≌△ADF（AAS），
∴AB=AD，
∴四边形ABCD是菱形．
∴BC=AB，
∵
| AE |
| AB |
∴BC=AB=
| 1 |
| sinα |
∴重叠部分（图中阴影部分）的面积为：BC×AE=1×
| 1 |
| sinα |
| 1 |
| sinα |
故选：C．
点评：此题主要考查了菱形的判定与性质，以及三角函数的应用，关键是证明四边形ABCD是菱形，利用三角函数求出BC的长．
练习册系列答案
相关题目