题目内容
当|x+1|≤6时，函数y=x|x|-2x+1的最大值是________．
16
分析：解不等式|x+1|≤6求x的取值范围，再根据x≥0，x＜0，把函数y=x|x|-2x+1去绝对值，在两种情况下，分别求出函数的最大值，比较即可．
解答：由|x+1|≤6解得-7≤x≤5，
当 0≤x≤5时，y=x2-2x+1，即y=（x-1）2，此时y最大=（5-1）2=16，
当-7≤x＜0时，y=-x2-2x+1，即y=2-（x+1）2，此时y最大=2，
因此，当-7≤x≤5时，y的最大值是16．
故本题答案为16．
点评：本题考查了二次函数最值的求法．关键是根据自变量的取值范围，分别求出最大值并进行比较．
分析：解不等式|x+1|≤6求x的取值范围，再根据x≥0，x＜0，把函数y=x|x|-2x+1去绝对值，在两种情况下，分别求出函数的最大值，比较即可．
解答：由|x+1|≤6解得-7≤x≤5，
当 0≤x≤5时，y=x2-2x+1，即y=（x-1）2，此时y最大=（5-1）2=16，
当-7≤x＜0时，y=-x2-2x+1，即y=2-（x+1）2，此时y最大=2，
因此，当-7≤x≤5时，y的最大值是16．
故本题答案为16．
点评：本题考查了二次函数最值的求法．关键是根据自变量的取值范围，分别求出最大值并进行比较．
练习册系列答案
阅读快车系列答案
相关题目
11、一列长为120米的火车匀速行驶，经过一条长为160米的隧道，从车头驶入隧道入口到车尾离开隧道出口公用14秒，设车头驶入隧道入口x秒时，火车在隧道内的长度为y米．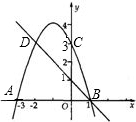
如图，已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点，与y轴交于点C，且点C、D是抛物线上的一对对称点．