Question

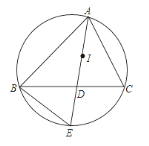
【题目】已知点E是菱形ABCD边BC上的中点，∠ABC＝30°，P是对角线BD上一点，且PC+PE＝．则菱形ABCD面积的最大值是_____．

Answer 1

【答案】20+8 ．

【解析】

取AB的中点E′，连接CE′交BD于P，由E、E′关于直线BD对称，推出PE=PE′，推出PE+PC=PE′+PC，所以当PC+PE′=CE′=时，菱形ABCD面积的最大，作E′H⊥BC于H，AM⊥BC于M．设AB=BC=2a，则AM=a，E′H=a，BH=a，CH=2a-a，在Rt△CHE′中，由CE′2=CH2+HE′2，可得26=a2+（2-）2a2，解得a2=，根据菱形ABCD面积的最大值=BCAM=2aa=2a2，由此即可解决问题．

取AB的中点E′，连接CE′交BD于P，

∵四边形ABCD是菱形，

∴∠ABD=∠CBD，∵BE=EC，

∴E、E′关于直线BD对称，

∴PE=PE′，

∴PE+PC=PE′+PC，

∴当PC+PE′=CE′=时，菱形ABCD面积的最大，

作E′H⊥BC于H，AM⊥BC于M．设AB=BC=2a，则AM=a，E′H=a，BH=a，CH=2a-a，

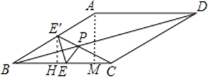
在Rt△CHE′中，∵CE′2=CH2+HE′2，

∴26=a2+（2-）2a2，

∴a2=，

∴菱形ABCD面积的最大值=BCAM=2aa=2a2=2×=20+8．

故答案为20+8．