Question

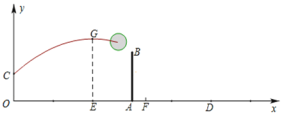
【题目】如图，在平面直角坐标系中，已知矩形的三个顶点、、．以为顶点的抛物线过点．动点从点出发，以每秒个单位的速度沿线段向点运动，运动时间为秒．过点作轴交抛物线于点，交于点．

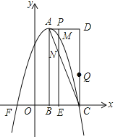
直接写出点的坐标，并求出抛物线的解析式；

当为何值时，的面积最大？最大值为多少？

Answer 1

【答案】（1）（2）1

【解析】

（1）根据矩形的性质可以写出点A得到坐标；由顶点A的坐标可设该抛物线的顶点式方程为y=a（x-1）2+4，然后将点C的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）；
（2）利用待定系数法求得直线AC的方程y=-2x+6；由图形与坐标变换可以求得点P的坐标（1，4-t），据此可以求得点E的纵坐标，将其代入直线AC方程可以求得点E或点G的横坐标；然后结合抛物线方程、图形与坐标变换可以求得GE=4-、点A到GE的距离为，C到GE的距离为2-；最后根据三角形的面积公式可以求得S△ACG=S△AEG+S△CEG=-（t-2）2+1，由二次函数的最值可以解得t=2时，S△ACG的最大值为1．

，

由题意知，可设抛物线解析式为

∵抛物线过点，

∴，

解得．

∴抛物线的解析式为，即；

∵，，

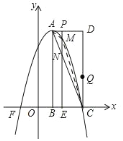
∴可求直线的解析式为．

∵点．

∴将代入中，解得点的纵坐标为，

∴把，代入抛物线的解析式中，可求点的纵坐标为，

∴，

又点到的距离为，到的距离为，

即

．

当时，的最大值为．