题目内容
(1999•烟台)如图,已知抛物线y=ax2+bx+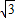 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
【答案】分析:根据抛物线的解析式,易求得C点的坐标,即可得到OC的长;可分别在Rt△OBC和Rt△OAC中,通过解直角三角形求出OB、OA的长,即可得到A、B的坐标,进而可运用待定系数法求得抛物线和直线的解析式.
解答:解:由题意得C(0,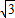 )
)
在Rt△COB中,
∵∠CBO=60°,
∴OB=OC•cot60°=1
∴B点的坐标是(1,0);(1分)
在Rt△COA中,∵∠CAO=45°,
∴OA=OC=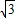
∴A点坐标( ,0)
,0)
由抛物线过A、B两点,
得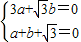 解得
解得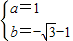
∴抛物线解析式为y=x2-(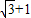 )x+
)x+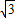 (4分)
(4分)
设直线BC的解析式为y=mx+n,
得n=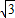 ,m=-
,m=-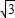
∴直线BC解析式为y=-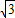 x+
x+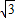 .(6分)
.(6分)
点评:此题主要考查的是用待定系数法求一次函数及二次函数解析式的方法.
解答:解:由题意得C(0,
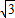 )
)在Rt△COB中,
∵∠CBO=60°,
∴OB=OC•cot60°=1
∴B点的坐标是(1,0);(1分)
在Rt△COA中,∵∠CAO=45°,
∴OA=OC=
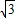
∴A点坐标(
 ,0)
,0)由抛物线过A、B两点,
得
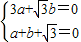 解得
解得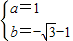
∴抛物线解析式为y=x2-(
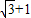 )x+
)x+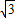 (4分)
(4分)设直线BC的解析式为y=mx+n,
得n=
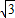 ,m=-
,m=-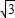
∴直线BC解析式为y=-
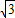 x+
x+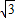 .(6分)
.(6分)点评:此题主要考查的是用待定系数法求一次函数及二次函数解析式的方法.

练习册系列答案
相关题目
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.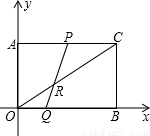
 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.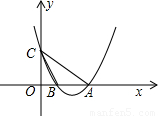
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.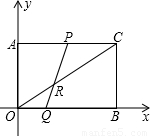
 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.