题目内容
（12分）在矩形纸片ABCD中，AB=6，BC=8，
（1）将矩形纸片沿BD折叠，使点A落在点E处（如图①），设DE和BC相交于点F，试说明△BDF为等腰三角形，并求BF的长；
（2）将矩形纸片折叠，使B与D重合（如图②）求折痕GH的长。
（1）
（2）
解析试题分析：设BF=x，由折叠的性质可知，DF=BF=x，CF=8-x，在Rt△CDF中，由勾股定理列方程求解
解：设BF=x，由折叠的性质可知，DF=BF=x，CF=8-x，在Rt△CDF中，CF2+CD2=DF2，即（8-x）2+62=x2，解得x=，即BF=
（2）B与D重合，则有，分析得出，GH=
考点：翻折变换（折叠问题）；勾股定理．
点评：本题考查了折叠的性质．关键是把已知线段与所求线段转化到直角三角形中，运用勾股定理解题
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
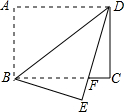在矩形纸片ABCD中，AB=6，BC=8．将矩形纸片沿BD折叠，使点A落在点E处，设DE与BC相交于点F，求BF的长．
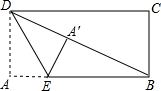（2013•太原）如图，在矩形纸片ABCD中，AB=12，BC=5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，则AE的长为
（2013•黄石模拟）如图，在矩形纸片ABCD中，AB=3，BC=4．把△BCD沿对角线BD折叠，使点C落在E处，BE交AD于点F；
如图，在矩形纸片ABCD中，AB=6，BC=8，现将其沿EF对折，使得点C与点A重合，则AF的长为
动手操作：如图，在矩形纸片ABCD中，AB=3，AD=5．如图所示折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动．