题目内容
已知方程 有两个不同的实数根,方程
有两个不同的实数根,方程 也有两个不同的实数根,且其两根介于方程
也有两个不同的实数根,且其两根介于方程 的两根之间,求k的取值范围.
的两根之间,求k的取值范围.
【答案】
a-4<k <a 2 .
【解析】
试题分析:一方面由一元二次方程根的判别式得出k <a 2;另一方面由二次函数y1=x 2+2ax+a-4和y2=x 2+2ax+k,它们的对称轴相同,且与x轴都有两个不同的交点,从而根据y2与x轴的两个交点都在y1与x轴的两个交点之间得到y2与y轴的交点在y1与y轴的交点上方,即k >a-4.
试题解析:∵方程 有两个不同的实数根,
有两个不同的实数根,
∴△1>0,而△1=4a 2-4(a-4)=4(a- )2+15≥15.
)2+15≥15.
又∵方程x 2+2ax+k=0也有两个不同的实数根,
∴△2=4a 2-4k>0,即k <a 2 .
对于二次函数y1=x 2+2ax+a-4和y2=x 2+2ax+k,它们的对称轴相同,且与x轴都有两个不同的交点,
∵y2与x轴的两个交点都在y1与x轴的两个交点之间,
∴y2与y轴的交点在y1与y轴的交点上方,如图.
∴k >a-4 .
∴k的取值范围是:a-4<k <a 2 .

考点:1.一元二次方程根的判别式;2. 一元二次方程与二次函数的关系;3.数形结合思想的应用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目







 有两个不同的实数解
有两个不同的实数解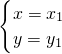 和
和 ,
, 的值.
的值.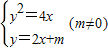 有两个不同的实数解
有两个不同的实数解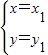 和
和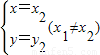 ,
,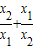 的值.
的值. 有两个不同的实数解
有两个不同的实数解 和
和 ,
, 的值.
的值.