题目内容
已知在△ABC中,∠A:∠B:∠C=1:2:3,以B为圆心,BC为半径的⊙B与AC边的位置关系是
- A.相离
- B.相切
- C.相交
- D.不确定
B
分析:先求出各个内角的度数确定直角后,可知AC、CB为直角边,所以可确定BC为半径的⊙B与AC边的位置关系是相切.
解答:∵在△ABC中,∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴以B为圆心,BC为半径的⊙B与AC边的位置关系是相切.
故选B.
点评:直线和圆的位置关系的确定一般是利用圆心到直线的距离与半径比较来判断.若圆心到直线的距离是d,半径是r,则①d>r,直线和圆相离,没有交点;②d=r,直线和圆相切,有一个交点;③d<r,直线和圆相交,有两个交点.本题需要先确定直角后再判断位置关系.
分析:先求出各个内角的度数确定直角后,可知AC、CB为直角边,所以可确定BC为半径的⊙B与AC边的位置关系是相切.
解答:∵在△ABC中,∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴以B为圆心,BC为半径的⊙B与AC边的位置关系是相切.
故选B.
点评:直线和圆的位置关系的确定一般是利用圆心到直线的距离与半径比较来判断.若圆心到直线的距离是d,半径是r,则①d>r,直线和圆相离,没有交点;②d=r,直线和圆相切,有一个交点;③d<r,直线和圆相交,有两个交点.本题需要先确定直角后再判断位置关系.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.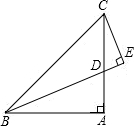 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.