题目内容
如图在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连接EB交OD于点F.(1)求证:OD⊥BE;
(2)若DE=
 ,AB=5,求AE的长.
,AB=5,求AE的长.
【答案】分析:(1)连AD,由AB为⊙O的直径,根据圆周角定理的推论得到AD⊥BC,AE⊥BE,而AB=AC,根据等腰三角形的性质有BD=DC,易得OD为△BAC的中位线,则OD∥AC,即可得到结论;
(2)OD⊥BE,根据垂径定理得弧BD=弧DE,则DB=DE= ,设OF=x,则DF=
,设OF=x,则DF= -x,利用勾股定理可得(
-x,利用勾股定理可得( )2-(
)2-( -x)2=(
-x)2=( )2-x2,解得x=
)2-x2,解得x= ,易证得OF为△BAE的中位线,则有AE=2OF=2×
,易证得OF为△BAE的中位线,则有AE=2OF=2× =3.
=3.
解答:(1)证明:连AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,∠AEB=90°,
∴AD⊥BC,AE⊥BE,
∵AB=AC,
∴BD=DC,
∵BO=OA,
∴OD为△BAC的中位线,
∴OD∥AC,
∴OD⊥BE;
(2)解:∵OD⊥BE,
∴弧BD=弧DE,
∴DB=DE= ,
,
∵AB=5,则OB=OD= ,
,
设OF=x,则DF= -x,
-x,
∵BF2=BD2-DF2=OB2-OF2,即( )2-(
)2-( -x)2=(
-x)2=( )2-x2,解得x=
)2-x2,解得x= ,
,
∵OF∥AE,OA=OB,
∴AE=2OF=2× =3.
=3.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了圆周角定理的推论、等腰三角形的性质以及勾股定理.
(2)OD⊥BE,根据垂径定理得弧BD=弧DE,则DB=DE=
 ,设OF=x,则DF=
,设OF=x,则DF= -x,利用勾股定理可得(
-x,利用勾股定理可得( )2-(
)2-( -x)2=(
-x)2=( )2-x2,解得x=
)2-x2,解得x= ,易证得OF为△BAE的中位线,则有AE=2OF=2×
,易证得OF为△BAE的中位线,则有AE=2OF=2× =3.
=3.解答:(1)证明:连AD,如图,

∵AB为⊙O的直径,
∴∠ADB=90°,∠AEB=90°,
∴AD⊥BC,AE⊥BE,
∵AB=AC,
∴BD=DC,
∵BO=OA,
∴OD为△BAC的中位线,
∴OD∥AC,
∴OD⊥BE;
(2)解:∵OD⊥BE,
∴弧BD=弧DE,
∴DB=DE=
 ,
,∵AB=5,则OB=OD=
 ,
,设OF=x,则DF=
 -x,
-x,∵BF2=BD2-DF2=OB2-OF2,即(
 )2-(
)2-( -x)2=(
-x)2=( )2-x2,解得x=
)2-x2,解得x= ,
,∵OF∥AE,OA=OB,
∴AE=2OF=2×
 =3.
=3.点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了圆周角定理的推论、等腰三角形的性质以及勾股定理.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

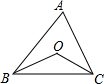 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是