题目内容
 如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为
如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为
- A.

- B.

- C.

- D.

B
分析:根据勾股定理列式求出AB、BC、AC,再利用勾股定理逆定理判断出△ABC是直角三角形,然后根据直角三角形斜边上的中线等于斜边的一半解答即可.
解答:根据勾股定理,AB= =
=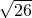 ,
,
BC= =2
=2 ,
,
AC=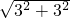 =3
=3 ,
,
∵AC2+BC2=AB2=26,
∴△ABC是直角三角形,
∵点D为AB的中点,
∴CD= AB=
AB= ×
×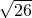 =
= .
.
故选B.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理,勾股定理逆定理的应用,判断出△ABC是直角三角形是解题的关键.
分析:根据勾股定理列式求出AB、BC、AC,再利用勾股定理逆定理判断出△ABC是直角三角形,然后根据直角三角形斜边上的中线等于斜边的一半解答即可.
解答:根据勾股定理,AB=
 =
=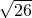 ,
,BC=
 =2
=2 ,
,AC=
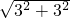 =3
=3 ,
,∵AC2+BC2=AB2=26,
∴△ABC是直角三角形,
∵点D为AB的中点,
∴CD=
 AB=
AB= ×
×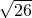 =
= .
.故选B.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理,勾股定理逆定理的应用,判断出△ABC是直角三角形是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 23、如图,每个小正方形的边长为单位长度1.
23、如图,每个小正方形的边长为单位长度1.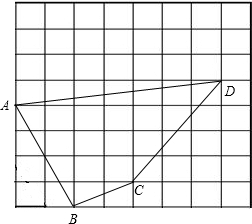 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1. 如图,每个小正方形的边长为1,则△ABC的面积等于
如图,每个小正方形的边长为1,则△ABC的面积等于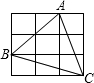 如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为
如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为 如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是
如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是