题目内容
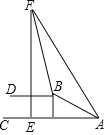
【题目】如图，斜坡AB坡度为1：2.4，长度为52米，在坡顶B所在的平台上有一座高楼EF，已知在A处测得楼顶F的仰角为60°，在B处测得楼顶F的仰角为77°，则高楼EF的高度是（ ）（精确到米，参考数据：sin77°≈0.97，tan77°≈4.33，
≈1.73）
A. 125米 B. 105米 C. 85米 D. 65米
【答案】A
【解析】
首先证明四边形BGEH是矩形，由题意BG：AG=1：2.4．在Rt△ABG中，根据AB=52米，由勾股定理可得BG=20米，AG=48米．在Rt△BHF中，可知tan77°=
，推出≈4.33，推出FH=4.33BH．在Rt△AEF中，由∠CAF=60°，可知EF=
AE，可得（48+BH）=20+4.33BH，解方程求出BH即可解决问题．
∵BG⊥AC，BH⊥EF，∴四边形BGEH是矩形，∴HB=EG，BG=HE，由题意得：BG：AG=1：2.4．在Rt△ABG中，∵AB=52米，由勾股定理可得：BG=20米，AG=48米．在Rt△BHF中，∵∠DBF=77°，∴tan77°=，∴≈4.33，∴FH=4.33BH．在△Rt△AEF中，∵∠CAF=60°，∴EF=AE，∴（48+BH）=20+4.33BH，解得：BH≈24.25，∴EF=（48+BH）≈125米．
故选A．
练习册系列答案
能考试全能100分系列答案
相关题目
