题目内容
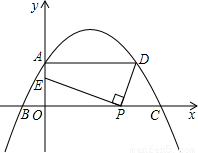
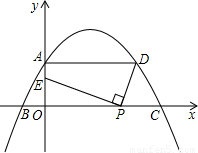
如图,二次函数过A(0,m)、B(-3,0)、C(12,0),过A点作x轴的平行线交抛物线于一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E。
(1)求AD的长;
(2)若在线段OC上存在不同的两点P1、P2,使相应的点E1、E2都与点A重合,试求m的取值范围;
(3)设抛物线的顶点为点Q,当60°≤∠BQC≤90°时,求m的变化范围。
(2)若在线段OC上存在不同的两点P1、P2,使相应的点E1、E2都与点A重合,试求m的取值范围;
(3)设抛物线的顶点为点Q,当60°≤∠BQC≤90°时,求m的变化范围。
| 解:(1)∵B(-3,0)、C(12,0)是关于抛物线对称轴对称的两点,AD∥x轴, ∴A、D也是关于抛物线对称轴对称的两点, ∵A(0,m),∴D(9,m),∴AD=9; |
 |
|
(2)∵PE⊥DP, |
|
| (3)设抛物线的方程为:y=a(x+3)(x-12), 又∵抛物线过点A(0,m), ∴m=-36a,∴a=-  m m ∴y=-  m(x+3)(x-12)=- m(x+3)(x-12)=- m(x- m(x- )2+ )2+ m m∵tan∠BQM=  ,QM= ,QM= m m又∵60°≤∠BQC≤90° ∴由抛物线性质得30°≤∠BQM≤45° ∴当∠BQM=30°时,可求出m=  , ,当∠BQM=45°时,可求出m=  , ,∴m的取值范围为  ≤m≤ ≤m≤ 。 。 |

练习册系列答案
相关题目
 ,∴|m|<
,∴|m|< ,
, ;
;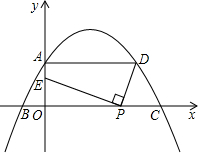 物线于一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E.
物线于一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E.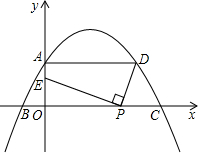 物线于一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E.
物线于一点D,线段OC上有一动点P,连接DP,作PE⊥DP,交y轴于点E.