Question

【题目】若正方形有两个相邻顶点在三角形的同一条边上，其余两个顶点分别在三角形的另两条边上，则正方形称为三角形该边上的内接正方形，△ABC中，设BC=a，AC=b，AB=c，各边上的高分别记为，，，各边上的内接正方形的边长分别记为，，．

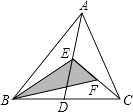
（1）模拟探究：如图，正方形EFGH为△ABC的BC边上的内接正方形，求证：；

（2）特殊应用：若∠BAC=90°，==2，求的值；

（3）拓展延伸：若△ABC为锐角三角形，b＜c，请判断与的大小，并说明理由．

Answer 1

【答案】（1）证明见解析；（2）；（3）＞．

【解析】

试题分析：（1）先根据EH∥FG，判定△AEH∽△ABC，再根据相似三角形对应边成比例，列出比例式变形即可得到；

（2）先根据（1）中的结论得出，再将=c和=2代入变形，即可求得的值；

（3）先根据（1）中的结论得出和，变形得出，，再根据△ABC得到b=c， =csinA，=bsinA，最后代入代数式进行变形推导，即可得出与的大小关系．

试题解析：∵正方形EFGH中，EH∥FG，∴△AEH∽△ABC，∵AD⊥BC，∴，即，∴；

（2）由（1）得：，∵∠A=90°，∴=c，又∵=2，∴=；

（3）＞．

证明：由（1）得：，，∴，，∵S=b=c，∴2S=b=c，又∵=csinA，=bsinA，∴==

=，∵b＜c，sinA＜1，∴＜0，即＜0，∴＞．