题目内容
【题目】如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长为 . 
【答案】10
【解析】解:连接AC、CF、AF,如图所示: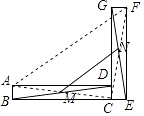
∵矩形ABCD绕点C顺时针旋转90°得到矩形FFCE,
∴∠ABC=90°,
∴AC= ![]() =
= ![]() =10
=10 ![]() ,
,
AC=BD=GE=CF,AC与BD互相平分,GE与CF互相平分,
∵点M、N分别是BD、GE的中点,
∴M是AC的中点,N是CF的中点,
∴MN是△ACF的中位线,
∴MN= ![]() AF,
AF,
∵∠ACF=90°,
∴△ACF是等腰直角三角形,
∴AF= ![]() AC=10
AC=10 ![]() ×
× ![]() =20,
=20,
∴MN=10.
故答案为:10.
连接AC、CF、AF,由矩形的性质和勾股定理求出AC,由矩形的性质得出M是AC的中点,N是CF的中点,证出MN是△ACF的中位线,由三角形中位线定理得出MN= ![]() AF,由等腰直角三角形的性质得出AF=
AF,由等腰直角三角形的性质得出AF= ![]() AC=20,即可得出结果.
AC=20,即可得出结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目